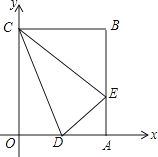
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线l平行于直线EC,且直线l与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线l上,则DF的长为 . 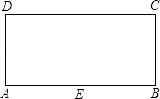
参考答案:
【答案】2 ![]() 或4﹣2
或4﹣2 ![]()
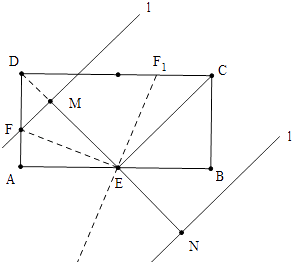
【解析】解:如图,当直线l在直线CE上方时,连接DE交直线l于M,
∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵AB=4,AD=BC=2,
∴AD=AE=EB=BC=2,
∴△ADE、△ECB是等腰直角三角形,
∴∠AED=∠BEC=45°,
∴∠DEC=90°,
∵l∥EC,
∴ED⊥l,
∴EM=2=AE,
∴点A、点M关于直线EF对称,
∵∠MDF=∠MFD=45°,
∴DM=MF=DE﹣EM=2 ![]() ﹣2,
﹣2,
∴DF= ![]() DM=4﹣2
DM=4﹣2 ![]() .
.
当直线l在直线EC下方时,
∵∠DEF1=∠BEF1=∠DF1E,
∴DF1=DE=2 ![]() ,
,
综上所述DF的长为2 ![]() 或4﹣2
或4﹣2 ![]() .
.
故答案为2 ![]() 或4﹣2
或4﹣2 ![]() .
.
本题考查翻折变换、矩形的性质、等腰直角三角形的性质和判定,解题的关键是正确画出图形,注意有两种情形,属于中考常考题型.当直线l在直线CE上方时,连接DE交直线l于M,只要证明△DFM是等腰直角三角形即可利用DF= ![]() DM解决问题,当直线l在直线EC下方时,由∠DEF1=∠BEF1=∠DF1E,得到DF1=DE,由此即可解决问题.
DM解决问题,当直线l在直线EC下方时,由∠DEF1=∠BEF1=∠DF1E,得到DF1=DE,由此即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.

(1)求证:AD=BC;
(2)若E、F、G、H分别是AB、CD、AC、BD的中点,求证:线段EF与线段GH互相垂直平分.
-
科目: 来源: 题型:
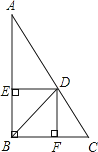
查看答案和解析>>【题目】已知:如图,△ABC中,∠ABC=90°,BD是∠ABC的平分线,DE⊥AB于点E , DF⊥BC于点F . 求证:四边形DEBF是正方形.
-
科目: 来源: 题型:
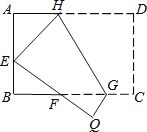
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是矩形ABCD各边的中点,AB=6,BC=8,则四边形EFGH的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积为cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),D是OA的中点,点E在AB上,当△CDE的周长最小时,点E的坐标为( )
A.(3,1)
B.(3, )
)
C.(3, )
)
D.(3,2)
相关试题

