【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.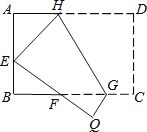
参考答案:
【答案】8
【解析】解:设AH=a,则DH=AD﹣AH=8﹣a,
在Rt△AEH中,∠EAH=90°,AE=4,AH=a,EH=DH=8﹣a,
∴EH2=AE2+AH2 , 即(8﹣a)2=42+a2 ,
解得:a=3.
∵∠BFE+∠BEF=90°,∠BEF+∠AEH=90°,
∴∠BFE=∠AEH.
又∵∠EAH=∠FBE=90°,
∴△EBF∽△HAE,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∵C△HAE=AE+EH+AH=AE+AD=12,
∴C△EBF= ![]() C△HAE=8.
C△HAE=8.
故答案为:8.
设AH=a,则DH=AD﹣AH=8﹣a,通过勾股定理即可求出a值,再根据同角的余角互补可得出∠BFE=∠AEH,从而得出△EBF∽△HAE,根据相似三角形的周长比等于对应比即可求出结论.本题考查了翻折变换、矩形的性质、勾股定理以及相似三角形的判定及性质,解题的关键是找出△EBF∽△HAE.本题属于中档题,难度不大,解决该题型题目时,通过勾股定理求出三角形的边长,再根据相似三角形的性质找出周长间的比例是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)试说明:AB∥CD;
(2)H是BE的延长线与直线CD的交点,BI平分∠HBD,写出∠EBI与∠BHD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠ADM的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,OF⊥OD。
(1)∠AOF与∠EOF相等吗?
(2)写出图中和∠DOE互补的角。
(3)若∠BOE=600,求∠AOD和∠EOF的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
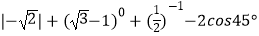 .
.
相关试题

