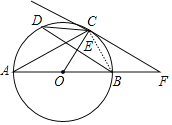
【题目】如图,AB为⊙O的直径,CD为⊙O的弦,连接AC,BD,半径CO交BD于点E,过点C作切线,交AB的延长线于点F,且∠CFA=∠DCA.

(1)求证:OE⊥BD;
(2)若BE=4,CE=2,则⊙O的半径是 ,弦AC的长是 .
参考答案:
【答案】(1)见解析;(2)5,4![]()
【解析】
(1)根据圆周角定理得到∠ABD=∠DCA,则∠CFA=∠ABD,则可判断BD∥CF,接着根据切线的性质得OC⊥CF,然后根据平行线的性质得到结论;
(2)连接BC,设⊙O的半径为r,在Rt△OBE中利用勾股定理得到(r﹣2)2+42=r2,求出r得到⊙O的半径为5,再利用勾股定理计算出BC=2![]() ,接着利用圆周角定理得到∠ACB=90°,然后利用勾股定理计算AC.
,接着利用圆周角定理得到∠ACB=90°,然后利用勾股定理计算AC.
(1)证明:∵∠CFA=∠DCA,∠ABD=∠DCA,
∴∠CFA=∠ABD,
∴BD∥CF,
∵CF为⊙O的切线,
∴OC⊥CF,
∴OC⊥BD,即OE⊥BD;
(2)解:如图,连接BC,
设⊙O的半径为r,则OE=r﹣2,OB=r,
在Rt△OBE中,(r﹣2)2+42=r2,
解得r=5,即⊙O的半径为5,
在Rt△BCE中,BC=![]() ,
,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC=![]() .
.
故答案为5,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加学校组织的智力竞答活动,竞赛中有两道单选题完全不会.这两道单选题各有A.B.C三个选项,第一道单选答案是B.第二道单选答案是C.最终两道题小明随机各写了一个答案
(1)小明答对第一道题的概率是 .
(2)请用树状图或者列表求出小明两道题都答对的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD是∠BAC的平分线,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
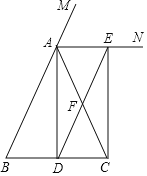
(1)求证:四边形ADCE为矩形;
(2)若矩形周长是18,且tan∠CAE=2,则四边形ABDF的周长是 .
-
科目: 来源: 题型:
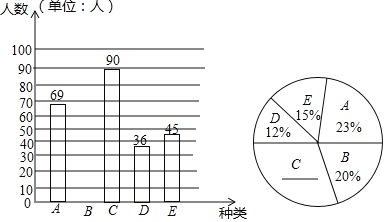
查看答案和解析>>【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC的顶点A的坐标为(0,1),点B的坐标为(1,2),∠ABC=90°,连接AC.
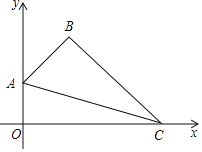
(1)求直线AC的函数表达式;
(2)点P是线段OC上一动点,从点O向点C运动,过点P作PM∥y轴,分别交AB或BC,AC于点M,N,其中点P的横坐标为m,MN的长为n.
①当0<m≤1时,求n与m之间的函数关系式;
②当△AMN的面积最大时,请直接写出m的值.
-
科目: 来源: 题型:
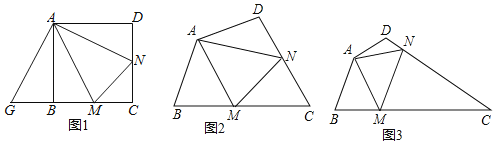
查看答案和解析>>【题目】(1)(探索发现)
如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为 .
(2)(类比延伸)
如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.
(3)(拓展应用)
如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=﹣
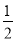 x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).
x2+bx+c与x轴交于点A,B,其中点B的坐标为(4,0),与y轴交于点C(0,2).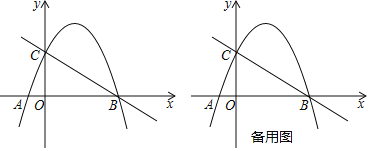
(1)求抛物线y=﹣
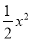 +bx+c和直线BC的函数表达式;
+bx+c和直线BC的函数表达式;(2)点P是直线BC上方的抛物线上一个动点,当点P到直线BC的距离最大时,求点P的坐标;
(3)连接点O与(2)中求出的点P,交直线BC于点D,点N是直线BC上的一个动点,连接ON,作DF⊥ON于点F,点F在线段ON上,当OD=
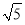 DF时,请直接写出点N的坐标.
DF时,请直接写出点N的坐标.
相关试题

