【题目】已知:△ABC内接于⊙O,D是 ![]() 上一点,OD⊥BC,垂足为H.
上一点,OD⊥BC,垂足为H. 
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
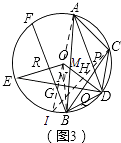
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5 ![]() ,BN=3
,BN=3 ![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求BF的长.
,求BF的长.
参考答案:
【答案】
(1)解:∵OD⊥BC,
∴由垂径定理可知:点H是BC的中点,
∵点O是AB的中点,
∴OH是△ABC的中位线,
∴AC=2OH;
(2)解:∵OD⊥BC,
∴由垂径定理可知: ![]() ,
,
∴∠BAD=∠CAD,
∵ ![]() ,
,
∴∠ABC=∠ADC,
∴180°﹣∠BAD﹣∠ABC=180°﹣∠CAD﹣∠ADC,
∴∠ACD=∠APB,
(3)解:连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,
∵∠ACD﹣∠ABD=2∠BDN,
∴∠ACD﹣∠BDN=∠ABD+∠BDN,
∵∠ABD+∠BDN=∠AND,
∴∠ACD﹣∠BDN=∠AND,
∵∠ACD+∠ABD=180°,
∴∠ABD+∠BDN=180°﹣∠AND,
∴∠AND=180°﹣∠AND,
∴∠AND=90°,
∵tan∠ABC= ![]() ,BN=3
,BN=3 ![]() ,
,
∴NQ= ![]() ,
,
∴由勾股定理可求得:BQ= ![]() ,
,
∵∠BNQ=∠QHD=90°,
∴∠ABC=∠QDH,
∵OE=OD,
∴∠OED=∠QDH,
∵∠ERG=90°,
∴∠OED=∠GBN,
∴∠GBN=∠ABC,
∵AB⊥ED,
∴BG=BQ= ![]() ,GN=NQ=
,GN=NQ= ![]() ,
,
∵AI是⊙O直径,
∴∠ACI=90°,
∵tan∠AIC=tan∠ABC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴IC=10 ![]() ,
,
∴由勾股定理可求得:AI=25,
连接OB,
设QH=x,
∵tan∠ABC=tan∠ODE ![]() ,
,
∴ ![]() ,
,
∴HD=2x,
∴OH=OD﹣HD= ![]() ﹣2x,
﹣2x,
BH=BQ+QH= ![]() +x,
+x,
由勾股定理可得:OB2=BH2+OH2,
∴( ![]() )2=(
)2=( ![]() +x)2+(
+x)2+( ![]() ﹣2x)2,
﹣2x)2,
解得:x= ![]() 或x=
或x= ![]() ,
,
当QH= ![]() 时,
时,
∴QD= ![]() QH=
QH= ![]() ,
,
∴ND=QD+NQ=6 ![]() ,
,
∴MN=3 ![]() ,MD=15
,MD=15
∵MD ![]() ,
,
∴QH= ![]() 不符合题意,舍去,
不符合题意,舍去,
当QH= ![]() 时,
时,
∴QD= ![]() QH=
QH= ![]()
![]()
∴ND=NQ+QD=4 ![]() ,
,
由垂径定理可求得:ED=10 ![]() ,
,
∴GD=GN+ND= ![]()
∴EG=ED﹣GD= ![]()
![]() ,
,
∵tan∠OED= ![]() ,
,
∴ ![]() ,
,
∴EG= ![]() RG,
RG,
∴RG= ![]() ,
,
∴BR=RG+BG=12
∴由垂径定理可知:BF=2BR=24.
【解析】本题考查圆的综合问题,涉及圆周角定理,中位线的性质,锐角三角函数,勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.(1)OD⊥BC可知点H是BC的中点,又中位线的性质可得AC=2OH;(2)由垂径定理可知: ![]() ,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;(3)由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC=
,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;(3)由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC= ![]() 可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=
可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED= ![]() 即可求得RG的长度,最后由垂径定理可求得BF的长度.
即可求得RG的长度,最后由垂径定理可求得BF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两支仪仗队各10名队员的身高(单位:cm)如下表:

(1)甲队队员的平均身高为 cm,乙队队员的平均身高为 cm;
(2)请用你学过的统计知识判断哪支仪仗队的身高更为整齐呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了改善住房条件,小亮的父母考察了某小区的
 两套楼房,
两套楼房, 套楼房在第
套楼房在第 层楼,
层楼, 套楼房在第
套楼房在第 层楼,
层楼, 套楼房的面积比
套楼房的面积比 套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设
套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设 套楼房的面积为
套楼房的面积为 平方米,
平方米, 套楼房的面积为
套楼房的面积为 平方米,根据以上信息列出了下列方程组.其中正确的是( ).
平方米,根据以上信息列出了下列方程组.其中正确的是( ).A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
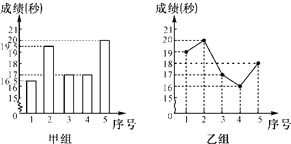
查看答案和解析>>【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀.这次竞赛中甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.

(1)求出下列成绩统计分析表中
 的值;
的值;(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组,但乙组同学不同意甲组同学的说法,认为他们的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对九(1)班学生进行百米测验,已知女生达标成绩为18秒,下面两图分别是甲、乙两小组各5名女生的成绩统计图.请你根据下面统计图回答问题.
(1)甲、乙两组的达标率分别是多少?
(2)根据图中信息你认为哪个组的成绩相对稳定?
(3)如果老师表扬甲组的成绩好于乙组,那么老师是从各组的平均数、中位数、达标率、方差中的哪个数来说明的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2.
(1)用尺规作图作出镜面BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系;
(3)你是如何思考的?

-
科目: 来源: 题型:
查看答案和解析>>【题目】情系灾区.5月12日我国四川汶川县发生里氏8.0级大地震,地震给四川,甘肃,陕西等地造成巨大人员伤亡和财产损失.灾难发生后,我校师生和全国人民一道,迅速伸出支援的双手,为灾区人民捐款捐物.为了支援灾区学校灾后重建,我校决定象灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套,一辆乙货车可装床架10个和课桌凳10套.
(1)学校如何安排甲、乙两种货车可一次性把这些物资运到灾区?有几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费最少?最少运费是多少?
相关试题

