【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转
,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转![]() 得到
得到![]() ,连
,连![]() ,则线段
,则线段![]() 的最小值为
的最小值为![]()
![]()

A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
参考答案:
【答案】C
【解析】过P'作P'E⊥AC于E,由旋转的性质及同角的余角相等,再用AAS判断出△DAP≌△P'ED,根据全等三角形对应边相等得出P'E=AD=2,当AP=DE=2时,DE=DC,即点E与点C重合,此时CP'=EP'=2,故线段CP′的最小值为2.
解:如图所示,过P'作P'E⊥AC于E,

则∠A=∠P'ED=90°,
由旋转可得,DP=P'D,∠PDP'=90°,
∴∠ADP=∠EP'D,
在△DAP和△P'ED中,
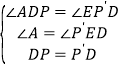 ,
,
∴△DAP≌△P'ED(AAS),
∴P'E=AD=2,
∴当AP=DE=2时,DE=DC,即点E与点C重合,
此时CP'=EP'=2,
∴线段CP′的最小值为2.
故选:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=5cm,BC=12cm.动点P从A点出发沿A→C的路径向终点C运动;动点Q从B点出发沿B→C→A路径向终点A运动.点P和点Q分别以每秒1cm和3cm的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥MN于E,QF⊥MN于F.则点P运动时间为_____秒时,△PEC与△QFC全等.
-
科目: 来源: 题型:
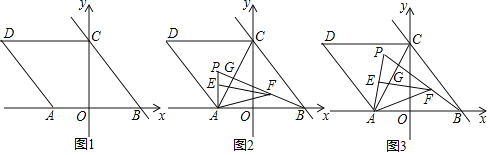
查看答案和解析>>【题目】已知:在平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,直线y=﹣
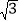 x+
x+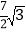 与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.(1)如图1,求点A的坐标;
(2)如图2,连接AC,点P为△ACD内一点,连接AP、BP,BP与AC交于点G,且∠APB=60°,点E在线段AP上,点F在线段BP上,且BF=AE,连接AF、EF,若∠AFE=30°,求AF2+EF2的值;
(3)如图3,在(2)的条件下,当PE=AE时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
,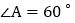 ,
,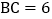 ,直线
,直线 ,且分别交边AB,AC于点M,N,已知直线MN将
,且分别交边AB,AC于点M,N,已知直线MN将 分为
分为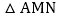 和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么
和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么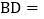 ______.
______.
-
科目: 来源: 题型:
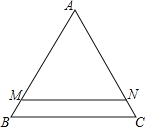
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
-
科目: 来源: 题型:
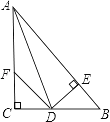
查看答案和解析>>【题目】如图,
 中,
中,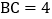 ,
,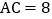 ,
,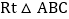 的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束
的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束 在这个运动过程中.
在这个运动过程中.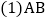 中点P经过的路径长______.
中点P经过的路径长______.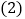 点C运动的路径长是______.
点C运动的路径长是______.
相关试题

