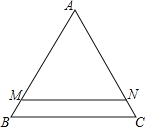
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,直线
,直线![]() ,且分别交边AB,AC于点M,N,已知直线MN将
,且分别交边AB,AC于点M,N,已知直线MN将![]() 分为
分为![]() 和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么
和梯形MBCN面积之比为5:1的两部分,如果将线段AM绕着点A旋转,使点M落在边BC上的点D处,那么![]() ______.
______.
参考答案:
【答案】![]()
【解析】过点A作AE⊥BC于点E,由AB=AC、∠A=60°,可得出△ABC为等边三角形,进而可得出BE、AE的长度,由MN∥BC可得出△AMN∽△ABC,根据相似三角形的性质结合直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,可求出AM的长度,由旋转的性质可得出AD的长度,在Rt△ADE中,利用勾股定理可求出DE的长度,再根据BD=BE±DE,即可求出BD的长度.
过点A作AE⊥BC于点E,如图所示.
∵AB=AC,∠A=60,
∴△ABC为等边三角形,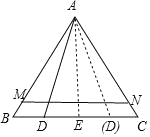
∴BE=CE=![]() BC=3,AE=
BC=3,AE=![]() BC=3
BC=3![]() .
.
∵MN∥BC,
∴△AMN∽△ABC,
∴![]() ,
,
∵直线MN将△ABC分为△AMN和梯形MBCN面积之比为5:1的两部分,
∴![]() =
=![]() ,即
,即![]() ,
,
解得:AM=![]() ,
,
∴AD=AM=![]()
在Rt△ADE中,∠AED=90,AD=![]() ,AE=3
,AE=3![]() .
.
∴DE=3![]() ,
,
∴BD=BE±DE=3±3![]()
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,点O为坐标原点,点A在x轴的负半轴上,直线y=﹣
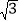 x+
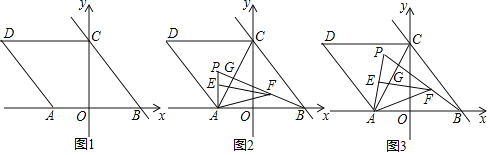
x+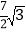 与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.
与x轴、y轴分别交于B、C两点,四边形ABCD为菱形.(1)如图1,求点A的坐标;
(2)如图2,连接AC,点P为△ACD内一点,连接AP、BP,BP与AC交于点G,且∠APB=60°,点E在线段AP上,点F在线段BP上,且BF=AE,连接AF、EF,若∠AFE=30°,求AF2+EF2的值;
(3)如图3,在(2)的条件下,当PE=AE时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,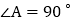 ,
,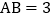 ,
,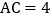 ,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转
,D为AC中点,P为AB上的动点,将P绕点D逆时针旋转 得到
得到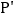 ,连
,连 ,则线段
,则线段 的最小值为
的最小值为
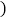

A.
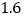 B.
B. 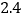 C. 2 D.
C. 2 D. 
-
科目: 来源: 题型:
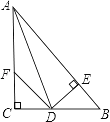
查看答案和解析>>【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
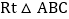 中,
中,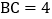 ,
,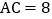 ,
,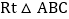 的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束
的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束 在这个运动过程中.
在这个运动过程中. 中点P经过的路径长______.
中点P经过的路径长______. 点C运动的路径长是______.
点C运动的路径长是______.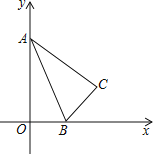
-
科目: 来源: 题型:
查看答案和解析>>【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰,为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如下尚不完整的统计图.
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
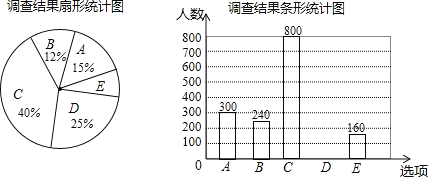
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有 人;
(2)扇形统计图中,扇形E的圆心角度数是 ;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
相关试题

