【题目】如图,反比例函数 ![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( ) 
A.1
B.2
C.3
D.4
参考答案:
【答案】C
【解析】解:由题意得:E、M、D位于反比例函数图象上,则S△OCE= ![]() ,S△OAD=
,S△OAD= ![]() , 过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
, 过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则 ![]() +
+ ![]() +9=4k,
+9=4k,
解得:k=3.
故选C.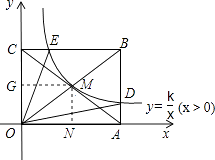
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为﹣4
D.抛物线与x轴的交点为(﹣1,0),(3,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是老师在嘉嘉的数学作业本上截取的部分内容:

问题:(1)这种解方程组的方法叫什么方法;嘉嘉的解法正确吗?如果不正确,从哪一步开始出错的?请你指出错误的原因,并求出正确的解.
(2)请用不同于(1)中的方法解这个方程组.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线y=﹣x2+3x上的概率为( )
A.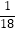
B.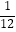
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程x2﹣(2m+3)x+m2+3m+2=0.
(1)已知x=2是方程的一个根,求m的值;
(2)以这个方程的两个实数根作为△ABC中AB、AC(AB<AC)的边长,当BC=
 时,△ABC是等腰三角形,求此时m的值.
时,△ABC是等腰三角形,求此时m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个公共汽车站相向发车,一人在街上行走,他发现每隔8分钟就迎面开来一辆公交车,每隔24分种从背后开来一辆公交车,如果车站发车的间隔时间相同,各车的速度相同,那两车站发车的间隔时间为( )
A. 18分钟 B. 10分钟 C. 12分钟 D. 16分钟
相关试题

