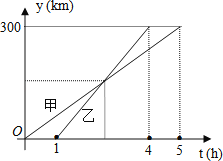
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=![]() 或
或![]() .
.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】B
【解析】
试题分析:观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
解:
由图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得![]() ,解得
,解得![]() ,
,
∴y乙=100t﹣100,
令y甲=y乙可得:60t=100t﹣100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲﹣y乙|=50,可得|60t﹣100t+100|=50,即|100﹣40t|=50,
当100﹣40t=50时,可解得t=![]() ,
,
当100﹣40t=﹣50时,可解得t=![]() ,
,
又当t=![]() 时,y甲=50,此时乙还没出发,
时,y甲=50,此时乙还没出发,
当t=![]() 时,乙到达B城,y甲=250;
时,乙到达B城,y甲=250;
综上可知当t的值为![]() 或
或![]() 或
或![]() 或t=
或t=![]() 时,两车相距50千米,
时,两车相距50千米,
∴④不正确;
综上可知正确的有①②共两个,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若另一组数据的标准差是2,则方差是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题,“若整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,则a,b,c中至少有一个偶数”. 第一步应假设______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
回答下列问题:
(1)规律验证:数轴上表示3和9两点之间的距离是__________,数轴上表示4和﹣3的两点之间的距离是__________;
(2)概念理解:数轴上表示x和﹣2的两点之间的距离表示为__________;
(3)拓展运用:若x表示一个有理数,|x﹣1|+|x+3|有最小值吗?若有,请直接写出最小值并说明x的范围;若没有,说出理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.
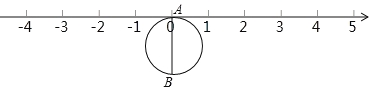
(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是__________数(填“无理”或“有理”),这个数是__________;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是__________;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B,C,D,E五名学生猜测自己的数学成绩. A说:“如果我得优,那么B也得优.” B说:“如果我得优,那么C也得优.” C说:“如果我得优,那么D也得优.” D说:“如果我得优,那么E也得优.” 大家都没有说错,但只有三个人得优,请问:得优的是哪三个人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年某县投入500万元用于该县的精准扶贫,预计到2018年该项投入将达720万元,若该项投入每年的增长率都为x,则下列方程正确的是( )
A.500(1+x)=720
B.500(1+x)2=720
C.500(1+x)+500(1+x)2=720
D.500x2=720
相关试题

