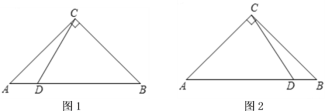
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点(不与点
边上的一个动点(不与点![]() ,
,![]() 及
及![]() 中点重合),连接
中点重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)如图1,当![]() 时,根据题意将图形补充完整,并直接写出
时,根据题意将图形补充完整,并直接写出![]() 的度数;
的度数;
(2)如图2,当![]() 时,用等式表示线段
时,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)作AH⊥CD延长于H,延长AH到E,使AH=HE,连接BE并延长BE,交CD延长线于F,可证明CF是AE的中垂线,即可得点E是点![]() 关于直线
关于直线![]() 的对称点,根据中垂线的性质及等腰三角形的性质即可求出∠BFC的度数;(2)由点
的对称点,根据中垂线的性质及等腰三角形的性质即可求出∠BFC的度数;(2)由点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() 可得
可得![]() ,即可证明
,即可证明![]() ,
,![]() ,
,![]() ,根据等腰三角形的性质可得
,根据等腰三角形的性质可得![]() ,进而可得
,进而可得![]() ,由
,由![]() 通过等量代换可知
通过等量代换可知![]() ,在
,在![]() 和Rt△ABC中,利用勾股定理即可证明结论.
和Rt△ABC中,利用勾股定理即可证明结论.
(1)如图:过点A作AH⊥CD延长于H,延长AH到E,使AH=HE,连接BE并延长BE,交CD延长线于F,
连接CE,
∵AH=EH,CH⊥AE,
∴CF是AE的中垂线,
∴点E是点![]() 关于直线
关于直线![]() 的对称点,
的对称点,
∴图形即为所求.
∵CF是AE的中垂线,
∴AC=CE,
∵∠ACD=15°,
∴∠ACE=30°,∠FCE=15°,
∵∠ACB=90°,
∴∠ECB=60°,
∵AC=BC,
∴CE=BC,
∴∠CEB=60°,
∴∠BFC=∠CEB-∠FCE=60°-15°=45°.
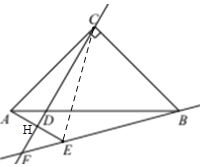
(2)猜想:![]() .
.
证明:连接![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,
,
∵点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线长为8
 ,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= . 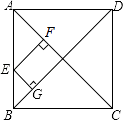
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角相等,即∠1=∠2.
如图②所示,AB,CD为两面平面镜,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你计算:图②中,当两平面镜AB,CD的夹角∠ABC是多少度时,可以使入射光线m与反射光线n平行但方向相反.
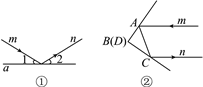
-
科目: 来源: 题型:
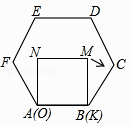
查看答案和解析>>【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5 -
科目: 来源: 题型:
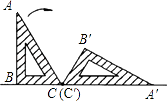
查看答案和解析>>【题目】如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为 cm.
-
科目: 来源: 题型:
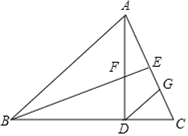
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.
相关试题

