【题目】平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角相等,即∠1=∠2.
如图②所示,AB,CD为两面平面镜,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你计算:图②中,当两平面镜AB,CD的夹角∠ABC是多少度时,可以使入射光线m与反射光线n平行但方向相反.
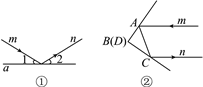
参考答案:
【答案】∠ABC=90°.
【解析】
根据平行线的判定得到:若使入射光线m与反射光线n平行,则∠5+∠6=180°,再由平角的定义及已知得到∠2+∠3=90°,根据三角形内角和定理求出∠ABC的度数即可.
由题意可知:∠1=∠2,∠3=∠4.
若使入射光线m与反射光线n平行,则∠5+∠6=180°.
∵∠1+∠2+∠5=180°,∠3+∠6+∠4=180°,∴∠1+∠2+∠3+∠4=180°,∴∠2+∠3=90°,∴在三角形ABC中,∠ABC=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC.
(1)证明:BC=DE;
(2)若AC=12,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=20°,则∠C的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线长为8
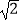 ,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= . 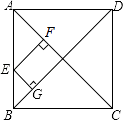
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
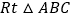 中,
中,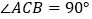 ,
,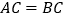 ,点
,点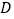 为
为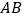 边上的一个动点(不与点
边上的一个动点(不与点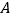 ,
,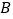 及
及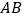 中点重合),连接
中点重合),连接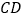 ,点
,点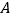 关于直线
关于直线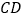 的对称点为点
的对称点为点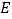 ,直线
,直线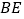 ,
,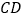 交于点
交于点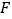 .
.(1)如图1,当
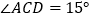 时,根据题意将图形补充完整,并直接写出
时,根据题意将图形补充完整,并直接写出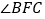 的度数;
的度数;(2)如图2,当
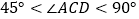 时,用等式表示线段
时,用等式表示线段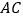 ,
,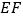 ,
,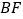 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.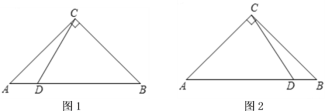
-
科目: 来源: 题型:
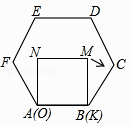
查看答案和解析>>【题目】已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作: 将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
A.1.4
B.1.1
C.0.8
D.0.5
相关试题

