【题目】如图,正方形ABCD的对角线长为8 ![]() ,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= . 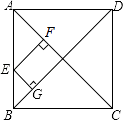
参考答案:
【答案】4 ![]()
【解析】解:如图:
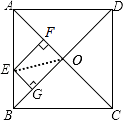
∵四边形ABCD是正方形,
∴OA=OB=4 ![]() ,
,
又∵S△ABO=S△AEO+S△EBO,
∴ ![]() OAOB=
OAOB= ![]() OAEF+
OAEF+ ![]() OBEG,
OBEG,
即 ![]() ×4
×4 ![]() ×4
×4 ![]() =
= ![]() ×4
×4 ![]() ×(EF+EG)
×(EF+EG)
∴EF+EG=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一个无理数筛选器的工作流程图.
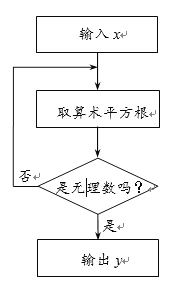
(1)当
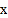 为16时,
为16时,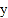 值为 ;
值为 ;(2)是否存在输入有意义的
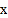 值后,却始终输不出
值后,却始终输不出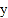 值?如果存在,写出所有满足要求的
值?如果存在,写出所有满足要求的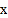 值;如果不存在,请说明理由;
值;如果不存在,请说明理由;(3)如果输入
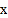 值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的
值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的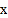 值可能是什么情况;
值可能是什么情况;(4)当输出的
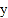 值是
值是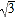 时,判断输入的
时,判断输入的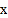 值是否唯一,如果不唯一,请写出其中的两个.
值是否唯一,如果不唯一,请写出其中的两个. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC.
(1)证明:BC=DE;
(2)若AC=12,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=20°,则∠C的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】平面镜反射光线的规律:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图①,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角相等,即∠1=∠2.
如图②所示,AB,CD为两面平面镜,经过两次反射后,入射光线m与反射光线n之间的位置关系会随之改变,请你计算:图②中,当两平面镜AB,CD的夹角∠ABC是多少度时,可以使入射光线m与反射光线n平行但方向相反.
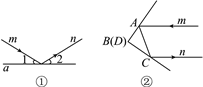
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
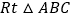 中,
中,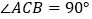 ,
,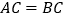 ,点
,点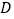 为
为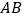 边上的一个动点(不与点
边上的一个动点(不与点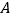 ,
,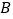 及
及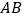 中点重合),连接
中点重合),连接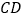 ,点
,点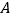 关于直线
关于直线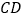 的对称点为点
的对称点为点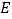 ,直线
,直线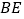 ,
,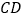 交于点
交于点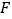 .
.(1)如图1,当
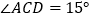 时,根据题意将图形补充完整,并直接写出
时,根据题意将图形补充完整,并直接写出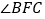 的度数;
的度数;(2)如图2,当
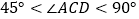 时,用等式表示线段
时,用等式表示线段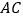 ,
,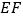 ,
,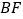 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.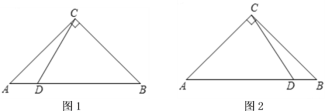
相关试题

