【题目】不能够铺满地面的组合图形是( )
A. 正八边形和正方形 B. 正方形和正三角形
C. 正六边形和正方形 D. 正六边形和正三角形
参考答案:
【答案】C
【解析】
正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解:A、正八边形和正方形内角分别为135°、90°,由于135×2+90=360,故能铺满,不符合题意;;
B、正三角形和正方形内角分别为60°、90°,由于60×3+90×2=360,故能铺满,不符合题意;
C、正方形的每个内角是90°,正六边形的每个内角是120°,90m+120n=360°,m=4-![]()
n,显然n取任何正整数时,m不能得正整数,故不能够铺满,符合题意;
D、正六边形的每个内角是120°,正三角形的每个内角是60°,由于2×120°+2×60°=360°,或120°+4×60°=360°,故能够铺满,不符合题意;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )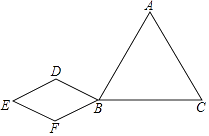
A.甲、乙都对
B.乙对甲不对
C.甲对乙不对
D.甲、乙都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:已知:A=2a2+3ab﹣2a﹣1,B=﹣a2+ab﹣1.
(1)求2A﹣3B;
(2)若A+2B的值与a的取值无关,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,抛物线y=
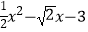 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.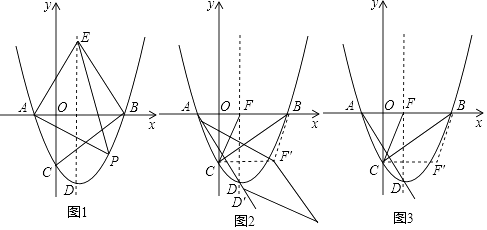
(1)求证:点E与点D关于x轴对称;
(2)点P为第四象限内的抛物线上的一动点,当△PAE的面积最大时,在对称轴上找一点M,在y轴上找一点N,使得OM+MN+NP最小,求此时点M的坐标及OM+MN+NP的最小值;
(3)如图2,平移抛物线,使抛物线的顶点D在射线AD上移动,点D平移后的对应点为D′,点A的对应点A′,设抛物线的对称轴与x轴交于点F,将△FBC沿BC翻折,使点F落在点F′处,在平面内找一点G,若以F′、G、D′、A′为顶点的四边形为菱形,求平移的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式变形中,正确的是( )
A.2x23x3=6x6
B.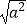 =a
=a
C.x2﹣4=(x+4)(x﹣4)
D.(a﹣b)2=(b﹣a)2
相关试题

