【题目】在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)AE与 MN的数量关系是:AE= MN ,BF与FG的数量关系是: BF= FG
【解析】(1)作辅助线,构建平行四边形PMND,再证明△ABE≌△DAP,即可得出结论;
(2)连接AG、EG、CG,构建全等三角形和直角三角形,证明AG=EG=CG,再根据四边形的内角和定理得∠AGE=90°,在R△AGE中,利用直角三角形斜边上的中线等于斜边的一半得BF=![]() AE,FG=
AE,FG=![]() AE,则BF=GF;
AE,则BF=GF;
(3)①AE=MN,证明△AEB≌△NMQ;
②BF=FG,同理得出BF和FG分别是直角△AEB和直角△AGF斜边上的中线,则 BF=![]() AE,FG=
AE,FG=![]() AE,所以BF=FG.
AE,所以BF=FG.
证明:
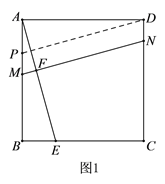
(1)在图1中,过点D作PD∥MN交AB于P,则∠APD=∠AMN
∵ 正方形ABCD
∴ AB = AD,AB∥DC,∠DAB =∠B = 90°
∴ 四边形PMND是平行四边形且PD = MN
∵ ∠B = 90° ∴∠BAE+∠BEA= 90°
∵MN⊥AE于F, ∴∠BAE+∠AMN = 90°
∴∠BEA =∠AMN =∠APD
又∵AB = AD,∠B =∠DAP = 90°
∴△ABE ≌ △DAP∴ AE = PD = MN
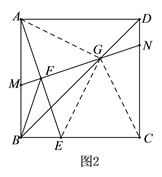
(2)在图2中连接AG、EG、CG
由正方形的轴对称性 △ABG ≌ △CBG∴ AG = CG,∠GAB=∠GCB
∵ MN⊥AE于F,F为AE中点∴ AG = EG
∴ EG = CG,∠GEC=∠GCE∴ ∠GAB=∠GEC
由图可知∠GEB+∠GEC=180°∴ ∠GEB+∠GAB =180°
又∵四边形ABEG的内角和为360°,∠ABE= 90°∴ ∠AGE = 90°
在Rt△ABE 和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=![]() AE, FG=
AE, FG= ![]() AE ∴BF= FG
AE ∴BF= FG
(3)AE与 MN的数量关系是:AE= MN
BF与FG的数量关系是: BF= FG
“点睛”本题是四边形的综合题,考查了正方形、全等三角形、平行四边形的性质与判定,在有中点和直角三角形的前提下,可以利用直角三角形斜边上的中线等于斜边的一半来证明两条线段相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与思考:
阅读理解问题——代数问题几何化 1.阅读理解以下文字: 我们知道,多项式的因式分解就是将一个多项式化成几个整 式的积的形式.通过因式分解,我们常常将一个次数比较高 的多项式转化成几个次数较低的整式的积,来达到降次化简 的目的.这个思想可以引领我们解决很多相对复杂的代数问 题.
例如:方程 2x2+3x=0 就可以这样来解:
解:原方程可化为 x(2x+3)=0,
所以x=0 或者 2x+3=0.
解方程 2x+3=0,得 x=-
 . ∴原方程的解为 x=0或x=-
. ∴原方程的解为 x=0或x=- .
. 根据你的理解,结合所学知识,解决以下问题:
(1)解方程:3x2-x=0
(2)解方程:(x+3)2-4x2=0;
(3)已知△ABC 的三边长为 4,x,y,请你判断代数式y2 -8y+16-x2的值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠A = ∠D,试说明 AC∥DE 成立的理由.

下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整。
解:∵ AB ∥ CD (已知)
∴ ∠A = (两直线平行,内错角相等)
又∵ ∠A = ∠D( )
∴ ∠ = ∠ (等量代换)
∴ AC ∥ DE ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
(2)如表是y与x的几组对应值
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
1
0
﹣1
﹣2
﹣1
0
m
…
①m等于多少;
②若A(n,2018),B(2020,2018)为该函数图象上不同的两点,则n等于多少;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并根据描出的点画出该函数的图象;根据函数图象可得:该函数的最小值为多少;该函数图象与x轴围成的几何图形的面积等于多少;
(4)已知直线y1=
 x﹣
x﹣ 与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.
与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .

(1)写出点D1的坐标;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2 , 若点D2(4,5),画出平移后的图形;
(3)求点D旋转到点D1所经过的路线长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?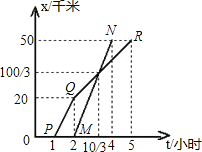
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
相关试题

