【题目】阅读与思考:
阅读理解问题——代数问题几何化 1.阅读理解以下文字: 我们知道,多项式的因式分解就是将一个多项式化成几个整 式的积的形式.通过因式分解,我们常常将一个次数比较高 的多项式转化成几个次数较低的整式的积,来达到降次化简 的目的.这个思想可以引领我们解决很多相对复杂的代数问 题.
例如:方程 2x2+3x=0 就可以这样来解:
解:原方程可化为 x(2x+3)=0,
所以x=0 或者 2x+3=0.
解方程 2x+3=0,得 x=-![]() . ∴原方程的解为 x=0或x=-
. ∴原方程的解为 x=0或x=-![]() .
.
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:3x2-x=0
(2)解方程:(x+3)2-4x2=0;
(3)已知△ABC 的三边长为 4,x,y,请你判断代数式y2 -8y+16-x2的值的符号.
参考答案:
【答案】(1)x1=0,x2=![]() (2)x1=-1,x2=3(3)符号为负.
(2)x1=-1,x2=3(3)符号为负.
【解析】
(1)根据因式分解即可求解(2)先用公式法因式分解即可求解;(3)先把y2 -8y+16-x2进行因式分解再利用三角形的三边关系进行求解.
(1)解方程:3x2-x=0
x(3x-1)=0
所以x=0 或者 3x-1=0.
x1=0,或x2=![]()
(2)解方程:(x+3)2-4x2=0;
[(x+3)+2x][(x+3)-2x]=0
(3x+3)(-x+3)=0,
3x+3=0或-x+3=0
x1=-1,或x2=3
(3)y2 -8y+16-x2= (y-4)2 -x2=(y-4+x)(y-4-x)
∵4,x,y,分别为△ABC 的三边长,
∴x+y-4>0,y-4-x<0,
故(y-4+x)(y-4-x)<0,
∴代数式y2 -8y+16-x2的值的符号为负.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某市区全民阅读状况进行调查和评估,有关部门随机抽取了部分市民进行每天阅读时间情况的调查,并根据调查结果制做了如下尚不完整的频数分布表(被调查者每天的阅读时间均在0﹣120分钟之内)
阅读时间x(分钟)
0≤x<30
30≤x<60
60≤x<90
90≤x≤120
频数
450
400
m
50
频率
0.45
0.4
0.1
n
(1)被调查的市民人数为多少,表格中,m,n为多少;
(2)补全频数分布直方图;
(3)某市区目前的常住人口约有118万人,请估计该市区每天阅读时间在60~120分钟的市民大约有多少万人?

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.

(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
-
科目: 来源: 题型:
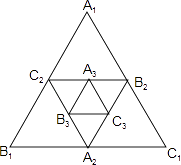
查看答案和解析>>【题目】如图,小强作出边长为1的第1个等边△A1B1C1 , 计算器面积为S1 , 然后分别取△A1B1C1三边的中点A2、B2、C1 , 作出第2个等边△A2B2C2 , 计算其面积为S2 , 用同样的方法,作出第3个等边△A3B3C3 , 计算其面积为S3 , 按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠A = ∠D,试说明 AC∥DE 成立的理由.

下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整。
解:∵ AB ∥ CD (已知)
∴ ∠A = (两直线平行,内错角相等)
又∵ ∠A = ∠D( )
∴ ∠ = ∠ (等量代换)
∴ AC ∥ DE ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
(2)如表是y与x的几组对应值
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
1
0
﹣1
﹣2
﹣1
0
m
…
①m等于多少;
②若A(n,2018),B(2020,2018)为该函数图象上不同的两点,则n等于多少;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并根据描出的点画出该函数的图象;根据函数图象可得:该函数的最小值为多少;该函数图象与x轴围成的几何图形的面积等于多少;
(4)已知直线y1=
 x﹣
x﹣ 与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.
与函数y=|x|﹣2的图象交于C,D两点,当y1≥y时,试确定x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3
相关试题

