【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则AK= .
,则AK= . 
参考答案:
【答案】2 ![]() ﹣3
﹣3
【解析】解:连接BH,如图所示:
∵四边形ABCD和四边形BEFG是正方形,
∴∠BAH=∠ABC=∠BEH=∠F=90°,
由旋转的性质得:AB=EB,∠CBE=30°,
∴∠ABE=60°,
在Rt△ABH和Rt△EBH中,![]() ,
,
∴Rt△ABH≌△Rt△EBH(HL),
∴∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,
∠ABE=30°,AH=EH,
∴AH=ABtan∠ABH= ![]() ×
× ![]() =1,
=1,
∴EH=1,
∴FH= ![]() ﹣1,
﹣1,
在Rt△FKH中,∠FKH=30°,
∴KH=2FH=2( ![]() ﹣1),
﹣1),
∴AK=KH﹣AH=2( ![]() ﹣1)﹣1=2
﹣1)﹣1=2 ![]() ﹣3;
﹣3;
故答案为:2 ![]() ﹣3.
﹣3.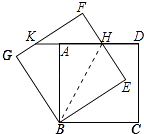
连接BH,由正方形的性质得出∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB,∠CBE=30°,得出∠ABE=60°,由HL证明Rt△ABH≌Rt△EBH,得出∠ABH=∠EBH= ![]() ∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.
∠ABE=30°,AH=EH,由三角函数求出AH,得出EH、FH,再求出KH=2FH,即可求出AK.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:
①abc>0
②4a+2b+c>0
③4ac﹣b2<8a
④ <a<
<a< 
⑤b>c.
其中含所有正确结论的选项是( )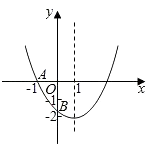
A.①③
B.①③④
C.②④⑤
D.①③④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△
 沿
沿 对折,叠合后的图形如图所示.若
对折,叠合后的图形如图所示.若 ,
, ,则∠2的度数为( )
,则∠2的度数为( )
A. 24° B. 35° C. 30° D. 25°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于______度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
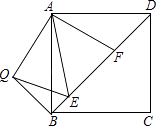
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2 .
相关试题

