【题目】如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: 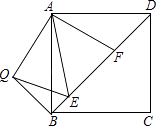
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2 .
参考答案:
【答案】
(1)证明:∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠ABQ=∠ADF=45°,
在△AQE和△AFE中
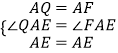 ,
,
∴△AQE≌△AFE(SAS),
∴∠AEQ=∠AEF,
∴EA是∠QED的平分线
(2)证明:由(1)得△AQE≌△AFE,
∴QE=EF,
在Rt△QBE中,
QB2+BE2=QE2,
则EF2=BE2+DF2.
【解析】(1)直接利用旋转的性质得出△AQE≌△AFE(SAS),进而得出∠AEQ=∠AEF,即可得出答案;(2)利用(1)中所求,再结合勾股定理得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为
 ,则AK= .
,则AK= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△
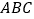 沿
沿 对折,叠合后的图形如图所示.若
对折,叠合后的图形如图所示.若 ,
, ,则∠2的度数为( )
,则∠2的度数为( )
A. 24° B. 35° C. 30° D. 25°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于______度.

-
科目: 来源: 题型:
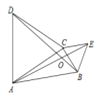
查看答案和解析>>【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
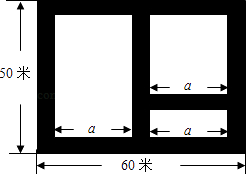
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=BC=2,D为BC的中点,在AC边上存在一点E,连结ED,EB,则△BDE周长的最小值为________.

相关试题

