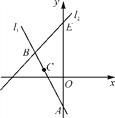
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
参考答案:
【答案】(1)y=-2x-3.(2) 13.5
【解析】(1)根据平移的性质得到点C的坐标;把点B、C的坐标代入直线方程y=kx+b(k≠0)来求该直线方程;
(2)根据点B的坐标求得直线l2的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答.
解:(1)由题意得:点C的坐标为(-2,1).
设直线l1的解析式为y=kx+c,
∵点B,C在直线l1上,
∴![]() ,
,
解得![]() ,
,
∴直线l1的解析式为y=-2x-3.
(2)把点B的坐标代入y=x+b,
得3=-3+b,
解得b=6,
∴y=x+6,
∴点E的坐标为(0,6),
∵直线y=-2x-3与y轴交于A点,
∴A的坐标为(0,-3),
∴AE=6+3=9,
∵B(-3,3),
∴S△ABE=![]() ×9×|-3|=13.5.
×9×|-3|=13.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.

(1)求证:BE=CE.
(2)求∠BEC的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
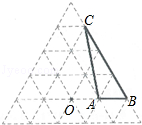
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别
时间t(小时)
人数
A
t≤0.5
5
B
0.5<t≤1
20
C
1<t≤1.5
a
D
1.5<t≤2
30
E
t>2
10
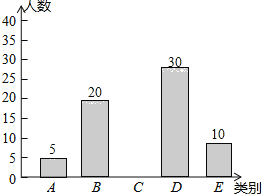
请根据图表信息解答下列问题:
(1)a= ;
(2)补全条形统计图;
(3)小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的时间在什么范围内?
(4)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;

(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;

(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(
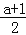 ☆3)☆(﹣
☆3)☆(﹣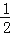 )=8,求a的值;
)=8,求a的值;(3)若2☆x=m,(
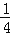 x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,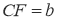 ,满足
,满足 .
.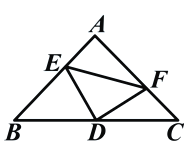
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
相关试题

