【题目】已知直线![]() :
:![]() 与函数
与函数![]() .
.
(1)直线![]() 经过定点
经过定点![]() ,直接写出点
,直接写出点![]() 的坐标:_______;
的坐标:_______;
(2)当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象存在唯一的公共点,在图
的图象存在唯一的公共点,在图![]() 中画出
中画出![]() 的函数图象并直接写出
的函数图象并直接写出![]() 满足的条件;
满足的条件;
(3)如图![]() ,在平面直角坐标系中存在正方形
,在平面直角坐标系中存在正方形![]() ,已知
,已知![]() 、
、![]() .请认真思考函数
.请认真思考函数![]() 的图象的特征,解决下列问题:
的图象的特征,解决下列问题:
①当![]() 时,请直接写出函数
时,请直接写出函数![]() 的图象与正方形
的图象与正方形![]() 的边的交点坐标:_______;
的边的交点坐标:_______;
②设正方形![]() 在函数
在函数![]() 的图象上方的部分的面积为
的图象上方的部分的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式.
的函数关系式.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)①交点坐标为
;(3)①交点坐标为![]() ,②
,②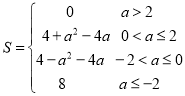 .
.
【解析】
(1)观察可知当x=-2时y=0,所以经过定点![]()
(2)先分类![]() 和
和![]() 讨论
讨论![]() ,分别得y=x,y=2-x,据此画出函数图象,再观察得出k的取值范围.
,分别得y=x,y=2-x,据此画出函数图象,再观察得出k的取值范围.
(3)①当![]() 时,
时,![]() ,画出图象观察即可得出答案.
,画出图象观察即可得出答案.
②分四种情况讨论.设![]() 与正方形交于
与正方形交于![]() 、
、![]() 两点.
两点.![]() 与正方形无交点;
与正方形无交点;![]() 点位于
点位于![]() 边上;
边上;![]() 点位于
点位于![]() 上时;
上时;![]() 点与
点与![]() 点重合.根据四种情况分别画出图形,进行计算.
点重合.根据四种情况分别画出图形,进行计算.
(1)观察可知当x=-2时y=0,所以经过定点![]()
(2)解:![]() 时
时![]() ,图象如图
,图象如图
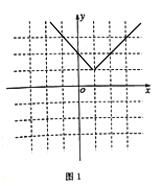
当![]() 或
或![]() 或
或![]() ,直线
,直线![]() 与函数
与函数![]() 的图象存在唯一的公共点,
的图象存在唯一的公共点,
(3)①当![]() 时,
时,![]() ,图象如图.
,图象如图.
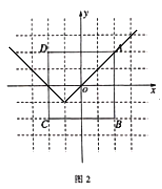
观察可知交点坐标为![]()
②解:由图象可知令顶点为![]()
![]() 与正方形交于
与正方形交于![]() 、
、![]() 两点
两点
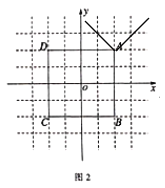
1)当![]() 时,
时,![]() 与正方形无交点,如下图所示,此时
与正方形无交点,如下图所示,此时![]() .
.
2)当![]() 时,
时,![]() 点位于
点位于![]() 边上
边上
![]()
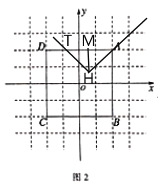
3)当![]() 时,
时,![]() 点位于
点位于![]() 上时
上时

![]()
![]()
4)当![]() 时,
时,![]() 点与
点与![]() 点重合
点重合
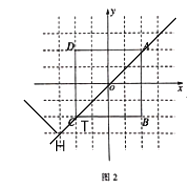
![]()
∴综上所述
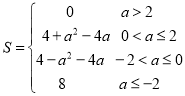
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E.过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为8,∠CDF=22.5°,求阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天)
1≤x<9
9≤x<15
x≥15
售价(元/斤)
第1次降价后的价格
第2次降价后的价格
销量(斤)
80﹣3x
120﹣x
储存和损耗费用(元)
40+3x
3x2﹣64x+400
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】武汉某文化旅游公司为了在军运会期间更好地宣传武汉,在工厂定制了一批具有浓郁的武汉特色的商品.为了了解市场情况,该公司向市场投放
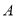 ,
,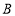 型商品共
型商品共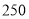 件进行试销,
件进行试销,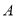 型商品成本价
型商品成本价 元/件,
元/件,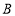 商品成本价
商品成本价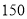 元/件,其中
元/件,其中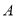 型商品的件数不大于
型商品的件数不大于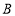 型的件数,且不小于
型的件数,且不小于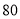 件,已知
件,已知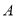 型商品的售价为
型商品的售价为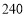 元/件,
元/件,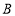 型商品的售价为
型商品的售价为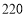 元/件,且全部售出.设投放
元/件,且全部售出.设投放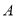 型商品
型商品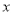 件,该公司销售这批商品的利润
件,该公司销售这批商品的利润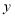 元.
元.(1)直接写出
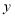 与
与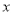 之间的函数关系式:_______;
之间的函数关系式:_______;(2)为了使这批商品的利润最大,该公司应该向市场投放多少件
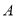 型商品?最大利润是多少?
型商品?最大利润是多少?(3)该公司决定在试销活动中每售出一件
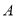 型商品,就从一件
型商品,就从一件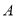 型商品的利润中捐献慈善资金
型商品的利润中捐献慈善资金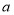 元,当该公司售完这
元,当该公司售完这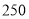 件商品并捐献资金后获得的最大收益为
件商品并捐献资金后获得的最大收益为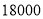 元时,求
元时,求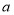 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 中,
中, ,求证:
,求证: ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:①∴
 ,这与三角形内角和为
,这与三角形内角和为 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴ ,③假设在
,③假设在 中,
中, ,④由
,④由 ,得
,得 ,即
,即 .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )A.③④②①B.③④①②C.①②③④D.④③①②
-
科目: 来源: 题型:
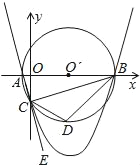
查看答案和解析>>【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC,BC,过A,B,C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连接BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
第三问改成,在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展以“迎新年”为主题的艺术活动,举办了四个项目的比赛.它们分别是:A演讲、B唱歌、C书法、D绘画.要求每位同学必须参加且限报一项.以九(一)班为样本进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给出的信息解答下列问题:
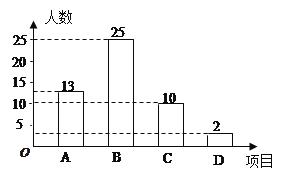
(1)求出参加绘画比赛的学生人数占全班总人数的百分比;
(2)求出扇形统计图中参加书法比赛的学生所在的扇形圆心角的度数;

(3)若该校九年级学生共有500人,请你估计这次活动中参加演讲和唱歌的学生共有多少人?
相关试题

