【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
参考答案:
【答案】(1)该种水果每次降价的百分率是10%;(2)y与x(1≤x<15)之间的函数关系式为:y=![]() ,第10天时销售利润最大;(3)第15天在第14天的价格基础上最多可降0.5元.
,第10天时销售利润最大;(3)第15天在第14天的价格基础上最多可降0.5元.
【解析】分析:(1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;
(2)根据两个取值先计算:当![]() 时和
时和![]() 时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比;
时销售单价,由利润=(售价-进价)×销量-费用列函数关系式,并根据增减性求最大值,作对比;
(3)设第15天在第14天的价格基础上最多可降![]() 元,根据第15天的利润比(2)中最大利润最多少127.5元,列不等式可得结论.
元,根据第15天的利润比(2)中最大利润最多少127.5元,列不等式可得结论.
详解:(1)设该种水果每次降价的百分率是x,
![]()
x=10%或x=190%(舍去),
答:该种水果每次降价的百分率是10%;
(2)当![]() 时,第1次降价后的价格:10×(110%)=9,
时,第1次降价后的价格:10×(110%)=9,
∴y=(94.1)(803x)(40+3x)=17.7x+352,
∵17.7<0,
∴y随x的增大而减小,
∴当x=1时,y有最大值,
y大=17.7×1+352=334.3(元),
当![]() 时,第2次降价后的价格:8.1元,
时,第2次降价后的价格:8.1元,
∴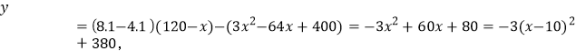
∵3<0,
∴当![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
当10<x<15时,y随x的增大而减小,
∴当x=10时,y有最大值,
y大=380(元),
综上所述,y与x(![]() )之间的函数关系式为:
)之间的函数关系式为:![]()
第10天时销售利润最大;
(3)设第15天在第14天的价格基础上最多可降a元,
由题意得:![]()
![]()
![]()
答:第15天在第14天的价格基础上最多可降0.5元.
-
科目: 来源: 题型:
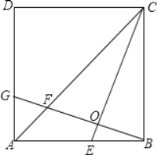
查看答案和解析>>【题目】如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.
-
科目: 来源: 题型:
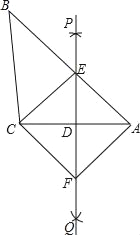
查看答案和解析>>【题目】已知:如图,在△ABC中,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:四边形AECF是菱形;
(2)若AD=3,AE=5,则求菱形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,王同学使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
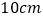 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A.
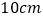 B.
B. 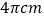 C.
C. 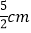 D.
D. 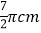
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=
 (k>1),求
(k>1),求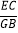 的值(用含k的式子表示).
的值(用含k的式子表示).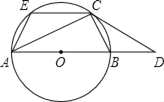
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知
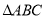 和互相垂直的两条直线
和互相垂直的两条直线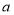 、
、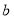 ,垂足为点
,垂足为点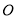 .
.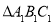 与
与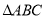 关于直线
关于直线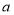 成轴对称,
成轴对称,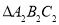 与
与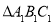 关于直线
关于直线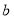 成对称.那么下列说法正确的是( )
成对称.那么下列说法正确的是( )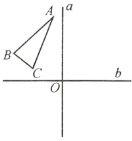
A.
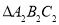 可以由
可以由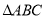 平移得到B.
平移得到B.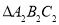 可以由
可以由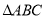 翻折得到
翻折得到C.
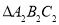 与
与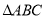 成轴对称D.
成轴对称D.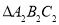 与
与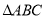 成中心对称
成中心对称 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
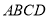 绕点
绕点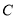 按逆时针方向旋转
按逆时针方向旋转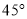 后得到图形
后得到图形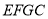 .请回答下列问题:
.请回答下列问题:(1)点
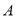 的对应点是点______,线段
的对应点是点______,线段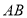 的对应线段是______,
的对应线段是______,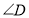 的对应角是______;
的对应角是______;(2)旋转中心是______,
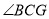 的大小是______,四边形
的大小是______,四边形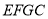 的形状是______;
的形状是______;(3)与线段
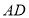 相等的线段有______.
相等的线段有______.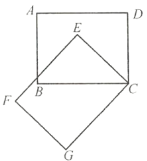
相关试题

