【题目】操作与证明:

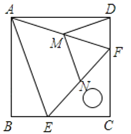
如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是: ;
拓展与探究:
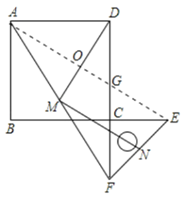
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)DM=MN,DM⊥MN;(3)成立,理由见解析.
【解析】
(1)先证明△ABE≌△ADF,再利用全等三角形的性质即可证明△AEF是等腰三角形;
(2)利用三角形中位线定理,直角三角形斜边中线定理可证明DM=MN,再证明∠DMN=∠DAB=90°,即可解决问题;
(3)连接AE,交DM于O,交CD于G,同(2)证明方法类似,可证明DM=MN,再证明∠DOG=∠ECG=90°,即可得出结论.
(1)证明:如图,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠ADF=90°,
∵△EFC是等腰直角三角形,
∴CE=CF,
∴BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
∴△AEF是等腰三角形;
(2)解:结论:DM=MN,DM⊥MN,
证明:∵在Rt△ADF中, M是AF的中点,
∴DM=![]() AF,
AF,
∵M是AF的中点,N是EF的中点,
∴MN=![]() AE,MN∥AE,
AE,MN∥AE,
∵AE=AF,
∴MN=DM,
∵∠ADF=90°,AM=MF,
∴MD=MA=MF,
∴∠MAD=∠ADM,
∴∠DMF=∠MAD+∠ADM=2∠DAM,
∵△ABE≌△ADF,
∴∠BAE=∠DAF,
∴∠DAB=∠EAF+2∠DAM=90°,
∵MN∥AE,
∴∠NMF=∠EAF,
∴∠DMN=∠NMF+∠DMF=∠EAF+2∠DAM=∠DAB=90°,
∴DM⊥MN,
∴MN=DM,MN⊥DM,
故答案为MN=DM,MN⊥DM;
(3)解:结论仍然成立.
理由:如图,连接AE,设AE交DM于O,交CD于G,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠ADF=90°,
又∵BC+CE=CD+CF,即BE=DF,
∴△ABE≌△ADF,
∴AF=AE,∠AFD=∠AEB,
∵在Rt△ADF中,M是AF的中点,
∴DM=![]() AF,
AF,
∵M是AF的中点,N是EF的中点,
∴MN=![]() AE,MN∥AE,
AE,MN∥AE,
∴MN=DM,
∵∠ADF=90°,AM=MF,
∴MD=MA=MF,
∴∠MDF=∠MFD=∠AEB,
∵∠DGO=∠CGE,∠ODG=∠CEG,
∴∠DOG=∠ECG=90°,
∵NM∥AE,
∴∠DOG=∠DMN=90°,
∴MN⊥DM,MN=DM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.

(1)若当t的值为m时,PP′恰好经过点A,求m的值.
(2)设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4)
(3)是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别
成本价/(元·箱
 )
)销售价/(元·箱
 )
)甲
25
35
乙
35
48
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a3+a2=2a5
B.(﹣2ab)3=﹣2ab3
C.2a3÷a2=2a
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 解方程:
解方程: ;
; 解方程:
解方程:
 解不等式组:
解不等式组: 并在数轴上表示出它的解集.
并在数轴上表示出它的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形中,由三角形的内角平分线所形成的角存在一定的规律,理解并掌握其中的规律,有助于同学们巩固相关的数学知识.
如图1,
 中,
中, 分别平分
分别平分 ,且相交于点
,且相交于点 “勤奋小组”的同学发现:
“勤奋小组”的同学发现: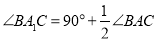 .证明过程如下:
.证明过程如下:
证明:如图2,连接
 并延长,
并延长,
则
 (依据1)
(依据1) 与
与 分别平分
分别平分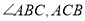
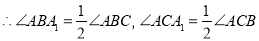




又
 ,(依据2)
,(依据2) .
. 依据1是 ___,依据2是 __;
依据1是 ___,依据2是 __; 如图3,在图1的基础上,作
如图3,在图1的基础上,作 的角平分线
的角平分线 交于点
交于点 试探究
试探究 与
与 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一水池有甲、乙、丙三个水管,其中甲、丙两管为进水管,乙管为出水管.单位时间内,甲管水流量最大,丙管水流量最小.先开甲、乙两管,一段时间后,关闭乙管开丙管,又经过一段时间,关闭甲管开乙管.则能正确反映水池蓄水量y(立方米)随时间t(小时)变化的图象是( )
A.
B.
C.
D.
相关试题

