【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以
方向以![]() 的速度向点
的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,请说明理由;
值;如果不能,请说明理由;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
参考答案:
【答案】(1)证明见详解(2)当![]() 时,四边形
时,四边形![]() 能够成为菱形;理由见详解(3)当
能够成为菱形;理由见详解(3)当![]() 或
或![]() 时,
时,![]() 为直角三角形;理由见详解
为直角三角形;理由见详解
【解析】
(1)根据时间和速度表示出![]() ,
,![]() ,再利用
,再利用![]() 角所对的直角边等于斜边的一半求得
角所对的直角边等于斜边的一半求得![]() ,则可得
,则可得![]() ,然后根据平行线的判定得到
,然后根据平行线的判定得到![]() ,即可得证结论;
,即可得证结论;
(2)由(1)的结论可得四边形![]() 是平行四边形,若
是平行四边形,若![]() 为菱形,则必有邻边相等,则
为菱形,则必有邻边相等,则![]() ,列出关于
,列出关于![]() 的方程求解即可;
的方程求解即可;
(3)当![]() 为直角三角形时,分三种情况分别找等量关系列方程求解即可.
为直角三角形时,分三种情况分别找等量关系列方程求解即可.
解:(1)根据题意得:![]() ,
,![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴四边形![]() 是平行四边形;
是平行四边形;
(2)结论:四边形![]() 能够成为菱形
能够成为菱形
理由:由(1)可知四边形![]() 是平行四边形
是平行四边形
若![]() 为菱形,则
为菱形,则![]() ,如图:
,如图:
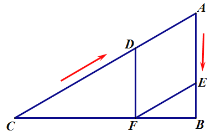
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴当![]() 时,四边形
时,四边形![]() 能够成为菱形;
能够成为菱形;
(3)①当![]() 时,如图:
时,如图:
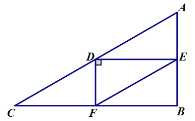
∵![]() ,
,![]()
∴四边形![]() 为矩形
为矩形
∴![]()
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∵由(1)可知![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
②当![]() 时,如图:
时,如图:
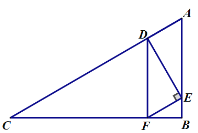
∵由(1)可知四边形![]() 是平行四边形
是平行四边形
∴![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]() ;
;
③当![]() 时,不成立;
时,不成立;
∴综上所述,当![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高速公路的同一侧有A、B两城镇,如图,它们到高速公路所在直线MN的距离分别为AA′=2 km,BB′=4 km,A′B′=8 km.要在高速公路上A′、B′之间建一个出口P,使A、B两城镇到P的距离之和最小.求这个最短距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.
班级
平均数(分)
中位数
众数
九(1)
85
85
九(2)
80
(1)根据图示填写上表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差,并说明哪个班级的成绩较稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置……,则正方形铁片连续旋转2020次后,点P的坐标为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1).
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1,L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣3,2),B(﹣4,1),C(﹣2,0).

(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)若△A2B2C2与△ABC是中心对称图形,则对称中心的坐标为 .
相关试题

