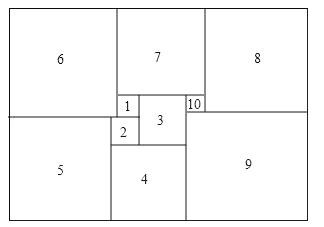
【题目】如图所示,1925年数学家莫伦发现的世界上第一个完美长方形,它恰能被分割成10个大小不同的正方形,请你计算:
(1)如果标注1、2的正方形边长分别为1,2,第3个正方形的边长= ;第5个正方形的边长= ;
(2)如果标注1、2的正方形边长分别为x,y,第10个正方形的边长= .(用含x、y的代数式表示)
参考答案:
【答案】(1)3,7;(2)3y﹣3x.
【解析】试题分析:(1)根据各个正方形的边的和差关系分别表示出第3个、第5个正方形的边长即可;
(2)根据各个正方形的边的和差关系分别表示出第3、4、5、6、7、10个正方形的边长即可.
试题解析:(1)观察图象可知第3个正方形的边长=3,第5个正方形的边长=7,
故答案为3,7;
(2)第3个正方形的边长是:x+y,
则第4个正方形的边长是:x+2y,
第5个正方形的边长是:x+2y+y=x+3y,
第6个正方形的边长是:(x+3y)+(y﹣x)=4y,
第7个正方形的边长是:4y﹣x,
第10个正方形的边长是:(4y﹣x)﹣x﹣(x+y)=3y﹣3x,
故答案为3y﹣3x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,y1)、B(2,y2)、C(﹣3,y3)在函数y=﹣2(x+1)2+3的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3
B.y1<y3<y2
C.y2<y3<y1
D.y3<y2<y1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
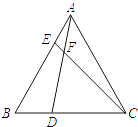
(1)求证:AD=CE;
(2)求∠DFC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形按一定规律排列,观察并回答:
(1)依照此规律,第四个图形共有★ 个,第六个图形共有★ 个;
(2)第n个图形中有★ 个;
(3)根据(2)中的结论,第几个图形中有2017个★?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区准备在每两幢楼房之间开辟绿地,其中有一块是面积为60m2的长方形绿地,并且长比宽多7m,求长方形的宽.若设长方形绿地的宽为xm,则可列方程为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1=37°36′,∠2=37.36°,则∠1与∠2的大小关系为( )
A.∠1<∠2
B.∠1=∠2
C.∠1>∠2
D.无法比较 -
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:

(1)如何进货,进货款恰好为46000元?
(2)为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?
相关试题

