【题目】如图,反比例函数y=![]() (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(1)求反比例函数的解析式;
(2)连接EF,求△BEF的面积.
参考答案:
【答案】解:(1)∵反比例函数y=![]() (k<0)的图象过点E(﹣1,2),
(k<0)的图象过点E(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函数的解析式为y=﹣![]() ;
;
(2)∵E(﹣1,2),
∴AE=1,OA=2,
∴BE=2AE=2,
∴AB=AE+BE=1+2=3,
∴B(﹣3,2).
将x=﹣3代入y=﹣![]() ,得y=
,得y=![]() ,
,
∴CF=![]() ,
,
∴BF=2﹣![]() =
=![]() ,
,
∴△BEF的面积=![]() BEBF=
BEBF=![]() ×2×
×2×![]() =
=![]() .
.
【解析】(1)将E(﹣1,2)代入y=![]() , 利用待定系数法即可求出反比例函数的解析式;
, 利用待定系数法即可求出反比例函数的解析式;
(2)由矩形的性质及已知条件可得B(﹣3,2),再将x=﹣3代入y=﹣![]() , 求出y的值,得到CF=
, 求出y的值,得到CF=![]() , 那么BF=2﹣
, 那么BF=2﹣![]() =
=![]() , 然后根据△BEF的面积=
, 然后根据△BEF的面积=![]() BEBF,将数值代入计算即可.
BEBF,将数值代入计算即可.
-
科目: 来源: 题型:
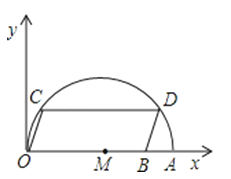
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,求点C的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=
 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离为|4﹣1|= ;表示5和﹣2两点之间的距离为|5﹣(﹣2)|=|5+2|= ;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|,如果表示数a和﹣2的两点之间的距离是3,那么a= .
(2)若数轴上表示数a的点位于﹣4与2之间,求|a+4|+|a﹣2|的值;
(3)当a= 时,|a+5|+|a﹣1|+|a﹣4|的值最小,最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.请根据信息解答下列问题:
(1)图1中淘米水浇花所在的扇形的圆心角度数为__________________;
(2)补全图2;
(3)求120名同学家庭月人均用水量的中位数和众数;
(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?

图1
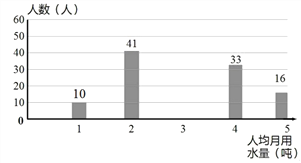
图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某中学准备在校园里利用围墙的一段,其余三面用围栏,围成一个矩形花园ABCD(围墙MN最长可利用25m).现计划用50m长的围栏,请你设计一种围法,使矩形花园的面积为300m2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:
 ≈1.41,
≈1.41, ≈1.73)
≈1.73)
相关试题

