搜索
【题目】“为了安全，请勿超速”．如图，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据：
≈1.41，
≈1.73）
参考答案：
【答案】解：此车没有超速．
理由：过C作CH⊥MN，
∵∠CBN=60°，BC=200米，
∴CH=BCsin60°=200×
=100
（米），
BH=BCcos60°=100（米），
∵∠CAN=45°，
∴AH=CH=100米，
∴AB=100﹣100≈73（m），
∵60千米/小时=
m/s，
∴
=14.6（m/s）＜≈16.7（m/s），
∴此车没有超速．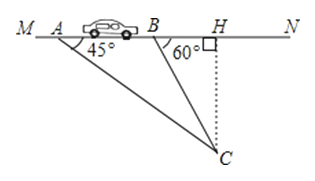
【解析】根据题意结合锐角三角函数关系得出BH，CH，AB的长进而求出汽车的速度，进而得出答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，反比例函数y=
（k＜0）的图象与矩形ABCD的边相交于E、F两点，且BE=2AE，E（﹣1，2）．
（1）求反比例函数的解析式；
（2）连接EF，求△BEF的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一，某校为了组织“节约用水从我做起”活动，随机调查了本校120名同学家庭月人均用水量和节水措施情况，如图1、图2是根据调查结果做出的统计图的一部分．请根据信息解答下列问题：
(1)图1中淘米水浇花所在的扇形的圆心角度数为__________________；
(2)补全图2；
(3)求120名同学家庭月人均用水量的中位数和众数；
(4)如果全校学生家庭总人数为3000人，根据这120名同学家庭月人均用水量，估计全校学生家庭月用水总量是多少吨？
图1
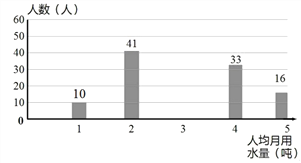
图2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某中学准备在校园里利用围墙的一段，其余三面用围栏,围成一个矩形花园ABCD（围墙MN最长可利用25m）.现计划用50m长的围栏，请你设计一种围法，使矩形花园的面积为300m2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣11，点B表示10，点C表示18，我们称点A和点C在数轴上相距29个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒．
问：（1）动点P从点A运动至C点需要多少时间？
（2）P、Q两点相遇时，求出相遇点M所对应的数是多少；
（3）求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%，90%．
（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低，并求出最低费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列两个等式：2﹣
＝2×+1，5﹣
＝5×+1，给出定义如下：我们称使等式a﹣b＝ab+1的成立的一对有理数a，b为“共生有理数对”，记为（a，b），如：数对（2，），（5，），都是“共生有理数对”．（1）数对（﹣2，1），（3，
）中是“共生有理数对”的是 ；（2）若（m，n）是“共生有理数对”，则（﹣n，﹣m） “共生有理数对”（填“是”或“不是”）；
（3）请再写出一对符合条件的“共生有理数对”为 ；（注意：不能与题目中已有的“共生有理数对”重复）
（4）若（a，3）是“共生有理数对”，求a的值．
相关试题
