【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
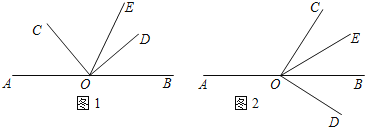
(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
参考答案:
【答案】(1)20°;(2)综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB
【解析】
(1)依据邻补角的定义以及角平分线的定义,即可得到∠COE的度数,进而得出∠DOE的度数;
(2)设∠AOC=α,则∠BOC=180°-α,依据OE平分∠BOC,可得∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
α,再分两种情况,依据∠COE=2∠DOB,即可得到∠AOC的度数.
(1)∵∠AOC=40°,
∴∠BOC=140°,
又∵OE平分∠BOC,
∴∠COE=![]() ×140°=70°,
×140°=70°,
∵∠COD=90°,
∴∠DOE=90°-70°=20°;
(2)设∠AOC=α,则∠BOC=180°-α,
∵OE平分∠BOC,
∴∠COE=![]() ×(180°-α)=90°-
×(180°-α)=90°-![]() α,
α,
分两种情况:
当OD在直线AB上方时,∠BOD=90°-α,
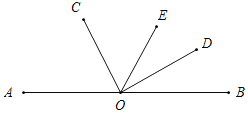
∵∠COE=2∠DOB,
∴90°-![]() α=2(90°-α),
α=2(90°-α),
解得α=60°.
当OD在直线AB下方时,∠BOD=90°-(180°-α)=α-90°,
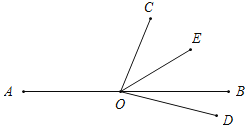
∵∠COE=2∠DOB,
∴90°-![]() α=2(α-90°),
α=2(α-90°),
解得α=108°.
综上所述,当∠AOC的度数是60°或108°时,∠COE=2∠DOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 ;将
;将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 ,连结
,连结 ,下列结论:①.
,下列结论:①. ;②.
;②. ;③.
;③.  .其中,正确的结论有__________________.(填上你认为正确的序号)
.其中,正确的结论有__________________.(填上你认为正确的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
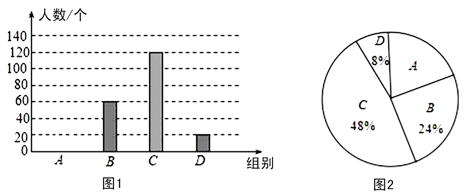
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)7(2x–1)–3(4x–1)=4(3x+2)–1;
(2)
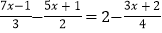 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
②若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y=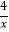 的图象上,则m<n.
的图象上,则m<n.
其中,正确命题的个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
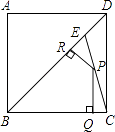
A.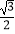
B.
C.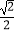
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是直线y=x与反比例函数y=
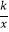 (k>0,x>0)的交点,B是y=
(k>0,x>0)的交点,B是y= 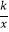 图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )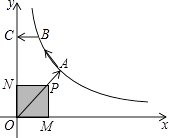
A.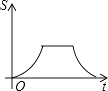
B.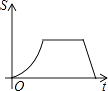
C.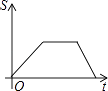
D.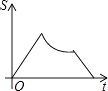
相关试题

