搜索
【题目】如图，已知点A是直线y=x与反比例函数y= 
（k＞0，x＞0）的交点，B是y= 图象上的另一点，BC//x轴，交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N．设四边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为（ ）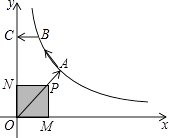
A.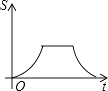
B.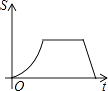
C.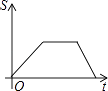
D.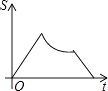
参考答案：
【答案】B
【解析】解：设点P的运动速度为v，
①由于点A在直线y=x上，
故点P在OA上时，四边形OMPN为正方形，
四边形OMPN的面积S= 
（vt）2 ，
②点P在反比例函数图象AB时，
由反比例函数系数几何意义，四边形OMPN的面积S=k；
③点P在BC段时，设点P运动到点C的总路程为a，
则四边形OMPN的面积=OC（a﹣vt）=﹣OCvt+OCa，
纵观各选项，只有B选项图形符合．
故选：B．
【考点精析】关于本题考查的函数的图象，需要了解函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．
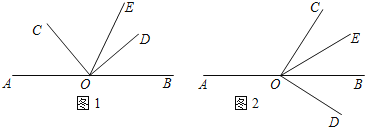
（1）如图（1），若∠AOC=
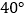，求∠DOE的度数；（2）如图（2），将∠COD绕顶点O旋转，且保持射线OC在直线AB上方，在整个旋转过程中，当∠AOC的度数是多少时，∠COE=2∠DOB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】给出下列四个命题：
①如果某圆锥的侧面展开图是半圆，则其轴截面一定是等边三角形；
②若点A在直线y=2x﹣3上，且点A到两坐标轴的距离相等，则点A在第一或第四象限；
③半径为5的圆中，弦AB=8，则圆周上到直线AB的距离为2的点共有四个；
④若A（a，m）、B（a﹣1，n）（a＞0）在反比例函y=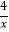
的图象上，则m＜n．
其中，正确命题的个数是（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值是（ ）
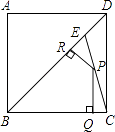
A.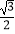
B.
C.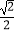
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图的数阵是由77个偶数排成：
（1）如图中任意作一个平行四边形框，设左上角的数为x，那么其他3个数从小到大可分别表示为 ．
（2）小红说这4个数的和是292，能求出这4个数吗？若存在，请求出这4个数．不存在说明理由．
（3）小明说4个数的和是420，存在这样的数吗？若存在，请求出这4个数，不存在说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见下图)，它符合规则：相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读理解：德国著名数学家高斯被认为是历史上最重要的数学家之一，并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出
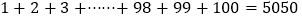，今天我们可以将高斯的做法归纳如下：令
①
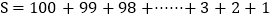②（右边相加100+1=2+99=3+98=…..=100+1共100组）
①＋②：有2S=101x100 解得：
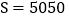
（1）请参照以上做法，回答，3+5+7+9+…..+97= ；
请尝试解决下列问题：
如下图，有一个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依此类推．
（2）填写下表：
层数
1
2
3
4
该层对应的点数
1
6
12
18
所有层的总点数的和
1
7
19
①写出第n层所对应的点数；（n≥2）
②如果某一层共96个点，求它是第几层；
③写出n层的六边形点阵的总点数.
相关试题
