【题目】在平面直角坐标系中,对于平面内任一点(a,b),若规定以下三种变换:
①△(a,b)=(﹣a,b);
②○(a,b)=(﹣a,﹣b);
③Ω(a,b)=(a,﹣b),
按照以上变换例如:△(○(1,2))=(1,﹣2),则○(Ω(3,4))等于 .
参考答案:
【答案】(﹣3,4)
【解析】解:○(Ω(3,4))=○(3,﹣4)=(﹣3,4).
所以答案是:(﹣3,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三种长度分别为三个连续整数的木棒,小明利用中等长度的木棒摆成了一个正方形,小刚用其余两种长度的木棒摆出了一个长方形,则他们两人谁摆的面积大?( )
A. 小刚 B. 小明 C. 同样大 D. 无法比较
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)
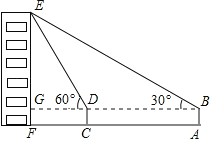
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
A. 正整数 、正分数、和0统称为有理数
B. 正整数、负整数统称为有理数
C. 正有理数、负有理数和0统称有理数
D. 0不是有理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果盈利20元记作+20,那么亏本50元记作( )
A.+50元
B.﹣50元
C.+20元
D.﹣20元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
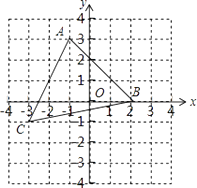
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
(2)点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(3)若网格上的每个小正方形的边长为1,则△ABC的面积是 .
相关试题

