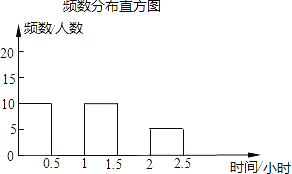
【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
请你将频数分布表和频数分布直方图补充完整.
参考答案:
【答案】图形见解析
【解析】
试题由所有频率之和为1求出未知的那个小组的频率,然后根据表格中已知的一组数据可以求出抽样调查的总人数,然后分别乘以各个所求小组的频率,就可以求出所有未知小组的频数,最后即可补全频数分布直方图.
试题解析:依题意得2≤t<2.5小组的频率为:1﹣0.2﹣0.4﹣0.2﹣0.1=0.1,
根据 0≤t<0.5这组数据可得抽样调查的总人数为10÷0.2=50人,
∴50×0.4=20人,
50×0.1=5人,
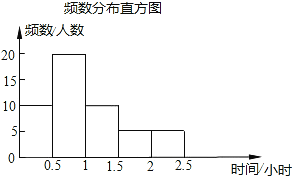
∴频数分布表和频数分布直方图补充如图所示:
时间分组(小时) | 频数(人数) | 频率 |
| 10 | 0.2 |
| 20 | 0.4 |
| 10 | 0.2 |
1.5≤t<2 | 5 | 0.1 |
2≤t<2.5 | 5 | 0.1 |
合计 | 50 | 1 |
-
科目: 来源: 题型:
查看答案和解析>>【题目】八年级(3)班共有学生54人,学习委员调查了班级学生参加课外活动的情况(每人只参加一项活动),其中:参加读书活动的18人,参加科技活动的人数占全班总人数的
 ,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )
,参加艺术活动的比参加科技活动的多3人,所调查班级同学参加体育活动情况如图所示,则在扇形图中表示参加体育活动人数的扇形的圆心角大小为( )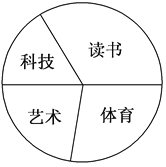
A. 100° B. 110°
C. 120° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连接CF

(1)如图1,当D点在BC上时,求证:①BE=2CF,②BE⊥CF.
(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明.如果不成立,请写出相应的正确的结论并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
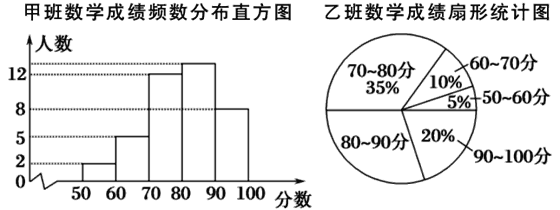
丙班数学成绩频数统计表
分数
50~60
60~70
70~80
80~90
90~100
人数
1
4
15
11
9
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
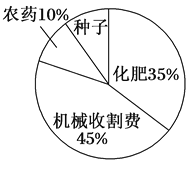
每亩生产成本
每亩产量
油菜籽市场价格
种植面积
110元
130千克
3元/千克
500 000亩
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.

(1)求a,c的值;
(2)连结OF,试判断△OEF是否为等腰三角形,并说明理由;
(3)现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等?若存在,直接写出点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在  上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32°
相关试题

