【题目】如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
(1)求a,c的值;
(2)连结OF,试判断△OEF是否为等腰三角形,并说明理由;
(3)现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上,一直角边始终过点E,另一直角边与y轴相交于点P,是否存在这样的点Q,使以点P,Q,E为顶点的三角形与△POE全等?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵△ABC为等腰直角三角形,
∴OA= ![]() BC.
BC.
又∵△ABC的面积= ![]() BC×OA=4,即OA2=4,
BC×OA=4,即OA2=4,
∴OA=2.
∴A(0,2),B(﹣2,0),C(2,0).
∴ ![]() ,
,
解得:  .
.
(2)
解:△OEF是等腰三角形.理由如下:如答图1,
∵A (0,2)),B (﹣2,0),
∴直线AB的函数表达式为:y=x+2,
又∵平移后的抛物线顶点F在射线BA上,
∴设顶点F的坐标为(m,m+2).
∴平移后的抛物线函数表达式为:y=﹣ ![]() (x﹣m)2+m+2.
(x﹣m)2+m+2.
∵抛物线过点C (2,0),
∴﹣ ![]() (x﹣m)2+m+2=0,解得m1=0,m2=6.
(x﹣m)2+m+2=0,解得m1=0,m2=6.
∴平移后的抛物线函数表达式为:y=﹣(x﹣6)2+8,
即y=﹣ ![]() x2+6x﹣10.
x2+6x﹣10.
当y=0时,﹣ ![]() x2+6x﹣10=0,
x2+6x﹣10=0,
解得x1=2,x2=10.
∴E(10,0),OE=10.
又∵F(6,8),OH=6,FH=8.
∴OF= ![]() =
= ![]() =10,
=10,
∴OE=OF,即△OEF为等腰三角形.

(3)
解:存在点Q(6,2 ![]() )或(6,3)或(10,12)或(4+
)或(6,3)或(10,12)或(4+ ![]() ,6+
,6+ ![]() )或(4﹣
)或(4﹣ ![]() ,6﹣
,6﹣ ![]() ),使以P,Q,E三点为顶点的三角形与△POE全等.
),使以P,Q,E三点为顶点的三角形与△POE全等.
理由如下:
点Q的位置分两种情形:
情形一:点Q在射线HF上,
当点P在x轴上方时,如答图2.
∵△PQE≌△POE,
∴QE=OE=10.
在Rt△QHE中,QH= ![]() =
= ![]() =2
=2 ![]() ,
,
∴Q(6,2 ![]() ).
).
当点P在x轴下方时,如答图3,有PQ=OE=10,
过P点作PK⊥HF于点K,则有PK=6.
在Rt△PQK中,QK= ![]() =
= ![]() =8,
=8,
∵∠PQE=90°,
∴∠PQK+∠HQE=90°.
∵∠HQE+∠HEQ=90°,
∴∠PQK=∠HEQ.
又∵∠PKQ=∠QHE=90°,
∴△PKQ∽△QHE.
∴ ![]() ,
,
即 ![]() ,
,
解得QH=3.
∴Q(6,3).
情形二:点Q在射线AF上,
当PQ=OE=10时,如答图4,有QE=PO,
∴四边形POEQ为矩形,
∴Q的横坐标为10.
当x=10时,y=x+2=12,
∴Q(10,12).
当QE=OE=10时,如答图5.
过Q作QM⊥y轴于点M,过E点作x轴的垂线交QM于点N,
设Q的坐标为(x,x+2),
∴MQ=x,QN=10﹣x,EN=x+2.
在Rt△QEN中,有QE2=QN2+EN2,
即102=(10﹣x)2+(x+2)2,
解得:x=4± ![]() .
.
当x=4+ ![]() 时,如答图5,y=x+2=6+
时,如答图5,y=x+2=6+ ![]() ,
,
∴Q(4+ ![]() ,6+
,6+ ![]() ).
).
当x=4﹣ ![]() 时,如答图6,y=x+2=6﹣
时,如答图6,y=x+2=6﹣ ![]() ,
,
∴Q(4﹣ ![]() ,6﹣
,6﹣ ![]() ).
).
综上所述,存在点Q(6,2 ![]() )或(6,3)或(10,12)或(4+
)或(6,3)或(10,12)或(4+ ![]() ,6+
,6+ ![]() )或(4﹣
)或(4﹣ ![]() ,6﹣
,6﹣ ![]() ),使以P,Q,E三点为顶点的三角形与△POE全等.
),使以P,Q,E三点为顶点的三角形与△POE全等.





【解析】(1)由△ABC为等腰直角三角形,且面积为4,易求得OA的长,即可求得点A,B,C的坐标,然后由待定系数法求得答案;(2)首先求得直线AB的函数表达式,设顶点F的坐标为(m,m+2),由抛物线过点C (2,0),可求得平移后的抛物线函数表达式,继而求得点E的坐标,即可判定△OEF是等腰三角形;(3)分别情形一:从点Q在射线HF上,当点P在x轴上方时或当点P在x轴下方时,以及情形二:点Q在射线AF上,去分析求解即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
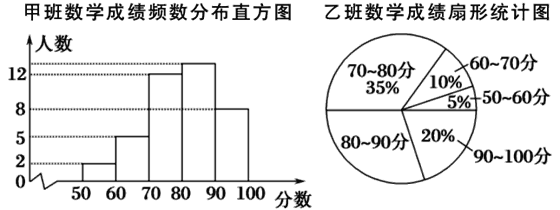
丙班数学成绩频数统计表
分数
50~60
60~70
70~80
80~90
90~100
人数
1
4
15
11
9
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
-
科目: 来源: 题型:
查看答案和解析>>【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时)
频数(人数)
频率
0≤t<0.5
10
0.2
0.5≤t<1
0.4
1≤t<1.5
10
0.2
1.5≤t<2
0.1
2≤t<2.5
5
合计
1
请你将频数分布表和频数分布直方图补充完整.
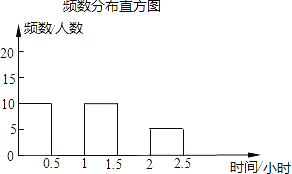
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
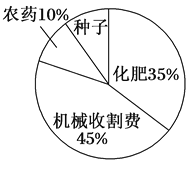
每亩生产成本
每亩产量
油菜籽市场价格
种植面积
110元
130千克
3元/千克
500 000亩
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在  上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32° -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
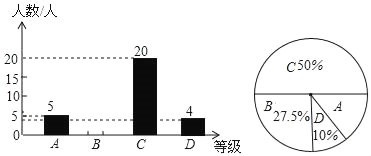
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD(四个边相等,四个角为直角)中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是( )
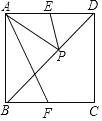
A. AB B. DE C. AF D. BD
相关试题

