【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是_____.

参考答案:
【答案】9 .
【解析】
过A点作AF⊥CD交CD的延长线于F点,由AE⊥BC,AF⊥CF,∠C=90°可得四边形AECF为矩形,则∠2+∠3=90°,而∠BAD=90°,根据等角的余角相等得∠1=∠3,加上∠AEB=∠AFD=90°和AB=AD,根据全等三角形的判定可得△ABE≌△ADF,由全等三角形的性质有AE=AF=5,S△ABE=S△ADF,则S四边形ABCD=S正方形AECF,然后根据正方形的面积公式计算即可.
过A点作AF⊥CD交CD的延长线于F点,如图:
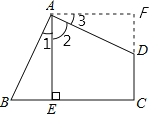
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
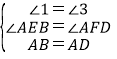
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案是:9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(
 )2017 B. 20×(
)2017 B. 20×( )2018 C. 20×(
)2018 C. 20×( )4036 D. 20×(
)4036 D. 20×( )4034
)4034 -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有_____个三角形出现.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD

(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣ |﹣2cos45°﹣(
|﹣2cos45°﹣(  )﹣1+(tan80°﹣
)﹣1+(tan80°﹣  )0+
)0+ 
(2)化简:( ﹣2)÷
﹣2)÷  ﹣2x,再代入一个合适的x求值.
﹣2x,再代入一个合适的x求值. -
科目: 来源: 题型:
查看答案和解析>>【题目】王杰同学在解决问题“已知A、B两点的坐标为A(3,﹣2)、B(6,﹣5)求直线AB关于x轴的对称直线A′B′的解析式”时,解法如下:先是建立平面直角坐标系(如图),标出A、B两点,并利用轴对称性质求出A′、B′的坐标分别为A′(3,2),B′(6,5);然后设直线A′B′的解析式为y=kx+b(k≠0),并将A′(3,2)、B′(6,5)代入y=kx+b中,得方程组
 ,解得
,解得 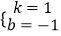 ,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( )
,最后求得直线A′B′的解析式为y=x﹣1.则在解题过程中他运用到的数学思想是( ) 
A.分类讨论与转化思想
B.分类讨论与方程思想
C.数形结合与整体思想
D.数形结合与方程思想 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形
 是半高三角形,且斜边
是半高三角形,且斜边 ,则它的周长等于_________.
,则它的周长等于_________.
相关试题

