搜索
【题目】点P(x ,y)在第一象限，且x+y=8 ，点A的坐标为(6，0).设三角形OPA的面积为S .
(1)用含x的解析式表示S ，写出 x的取值范围.
(2)当点P的横坐标为5的时候，三角形OPA的面积是多少？
参考答案：
【答案】(1)S=-3x+24，0< x < 8；(2)S=9.
【解析】
（1）根据三角形的面积公式列式，即可用含x的解析式表示S，然后根据S>0及已知条件，可求出x的取值范围；
（2）将x=5代入（1）中所求解析式，即可求出△OPA的面积．
(1)∵A和P点的坐标分别是(6,0)、(x,y)，
∴△OPA的面积=
OA|y|，
∴S=×6×|y|=3y.
∵x+y=8，∴y=8x.
∴S=3(8x)=243x=-3x+24；
∵S=3x+24>0，
解得：x<8；
又∵点P在第一象限，
∴x>0，
即x的范围为：0<x<8；
(2)∵S=3x+24，
∴当x=5时，S=3×5+24=9.
即当点P的横坐标为5时，△OPA的面积为9；故答案为：(1)S=-3x+24，0< x < 8；(2)S=9.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O，与斜边AB交于点D、E为BC边的中点，连接DE．
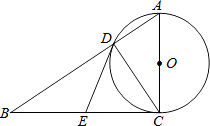
（1）求证：DE是⊙O的切线；
（2）填空：①若∠B=30°，AC=2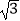
，则DE=； ②当∠B=°时，以O，D，E，C为顶点的四边形是正方形． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P等于________度（用含有α的式子表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠BAE +∠AED=180°，∠1=∠2，那么∠M=∠N．下面是推理过程，请你完成.
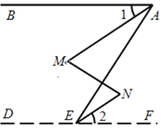
解：∵∠BAE+∠AED=180°（已知）
∴AB∥DE（______）.
∴∠BAE=∠AEF（______）.
又∵∠1=∠2（已知）
∴ ∠BAE∠1=∠AEF_____(等式性质)，即 ∠MAE = ∠NEA .
∴_______∥______（______）.
∴∠M=∠N（两直线平行，内错角相等）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为1个单位长度的小正方形组成的网格中．
（1）把△ABC平移至
的位置，使点A与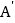对应，得到△
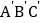；（2）图中可用字母表示，与线段
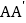平行且相等的线有：________；（3）求四边形
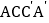的面积．
-
科目： 来源： 题型：
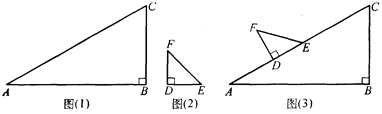
查看答案和解析>>【题目】某同学在一次课外活动中，用硬纸片做了两个直角三角形，见图(1)、图(2)．在图(1)中，∠B=90°，∠A=30°；图(2)中，∠D=90°，∠F=45°．图(3)是该同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上，移动开始时，点D与点A重合．
(1)△DEF在移动过程中，∠FCE与∠CFE度数之和是否为定值，请加以说明；
(2)能否将△DEF移动至某位置，使F、C的连线与AB平行?若能，求出∠CFE的度数；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，将矩形ABCD沿DE折叠，使顶点A落在DC上的点A′处，然后将矩形展平，沿EF折叠，使顶点A落在折痕DE上的点G处．再将矩形ABCD沿CE折叠，此时顶点B恰好落在DE上的点H处．如图2．
（1）求证：EG=CH；
（2）已知AF=
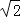，求AD和AB的长．
相关试题
