【题目】如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P等于________度(用含有α的式子表示)

参考答案:
【答案】![]()
【解析】
根据∠A+∠D=α,可得∠ABC+∠BCD=360°-α,然后根据PB、PC为角平分线,可求出∠PBC+∠PCB的度数,最后根据三角形的内角和定理求出∠P的度数.
∵四边形的内角和为(4-2)×180°=360°,
∴四边形ABCD中,∠ABC+∠BCD=360°-(∠A+∠D)=360°-α,
∵PB和PC分别为∠ABC、∠BCD的平分线,
∴∠PBC+∠PCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() (360°-α)=180°-
(360°-α)=180°-![]() α,
α,
则∠P=180°-(∠PBC+∠PCB)=180°-(180°-![]() α)=
α)=![]() α.
α.
故答案为:![]() α
α
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解方程:
(1) 3x2 -2x = 0; (2)

(3) x2 +2 x -5= 0; (4)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人
面试
笔试
形体
口才
专业水平
创新能力
甲
86
90
96
92
乙
92
88
95
93
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.
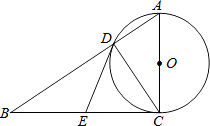
(1)求证:DE是⊙O的切线;
(2)填空:①若∠B=30°,AC=2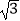 ,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形.
,则DE=; ②当∠B=°时,以O,D,E,C为顶点的四边形是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
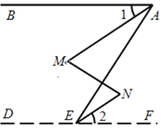
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE(______).
∴∠BAE=∠AEF(______).
又∵∠1=∠2(已知)
∴ ∠BAE∠1=∠AEF_____(等式性质),即 ∠MAE = ∠NEA .
∴_______∥______(______).
∴∠M=∠N(两直线平行,内错角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(x ,y)在第一象限,且x+y=8 ,点A的坐标为(6,0).设三角形OPA的面积为S .
(1)用含x的解析式表示S ,写出 x的取值范围.
(2)当点P的横坐标为5的时候,三角形OPA的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至
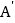 的位置,使点A与
的位置,使点A与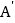 对应,得到△
对应,得到△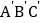 ;
;(2)图中可用字母表示,与线段
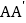 平行且相等的线有:________;
平行且相等的线有:________;(3)求四边形
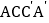 的面积.
的面积.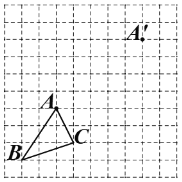
相关试题

