【题目】已知:如图,在平行四边形ABCD中,连接对角线BD,作AE⊥BD于E,CF⊥BD于F, 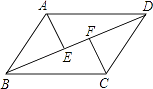
(1)求证:△AED≌△CFB;
(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四边形ABCD的周长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ADE=∠CBF,
又∵AE⊥BD于E,CF⊥BD于F,
∴∠AED=∠CFB=90°,
在△AED和△CFB中,
 ,
,
∴△AED≌△CFB (AAS)
(2)解:在Rt△AED中,
∵∠ADE=30°,AE=3,
∴AD=2AE=2×3=6,
∵∠ABC=75°,∠ADB=∠CBD=30°
∴∠ABE=45°,
在Rt△ABE中,
∵ ![]() =sin45°,
=sin45°,
∴AB= ![]() =3
=3 ![]() ,
,
∴平行四边形ABCD的周长l=2(AB+AD)=2×(6+3 ![]() )=12+6
)=12+6 ![]()
【解析】(1)在平行四边形ABCD中,AD=BC,AD∥BC,可知∠ADE=∠CBD,然后根据AE⊥BD于E,CF⊥BD于F,可知∠AED=∠CFB=90°,根据这三个条件即可证明全等;(2)根据已知∠ABC=75°,∠ADB=30°,AE=3,分别在Rt△ABE、Rt△AED中求出AB、AD的长度,即可求出周长.
【考点精析】利用平行四边形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
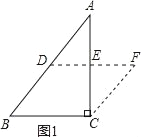
查看答案和解析>>【题目】在△ABC中,沿图示的中位线DE剪一刀,拼成如图1所示的平行四边形BCFD.请仿上述方法,按要求完成下列操作设计,并在规定位置画出图示:
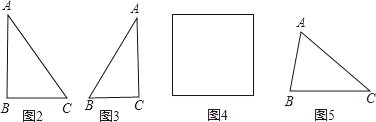
(1)在△ABC中,若∠C=90°,沿着中位线剪一刀,可拼成矩形或等腰梯形,请将拼成的图形画在图2位置(只需画一个);
(2)在△ABC中,若AB=2BC,沿着中位线剪一刀,可拼成菱形,并将拼成的图形画在图3位置;
(3)在△ABC中,需增加什么条件,沿着中位线剪一刀,拼成正方形,并将拼成的图形和符合条件的三角形一同画在图4位置;
(4)在△ABC中,若沿着某条线剪一刀,能拼成等腰梯形,请将拼成的图形画在图5位置(保留寻求剪裁线的痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】小学我们已经知道三角形三个内角和是180°,对于如图1中,
 ,
,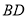 交于
交于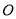 点,形成的两个三角形中的角存在以下关系:①
点,形成的两个三角形中的角存在以下关系:①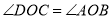 ;②
;②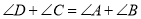 .试探究下面问题:
.试探究下面问题:已知
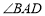 的平分线
的平分线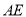 与
与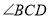 的平分线
的平分线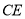 交于点
交于点 ,
,
(1)如图2,若
 ,
,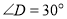 ,
,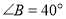 ,则
,则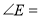 _________;
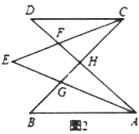
_________;(2)如图3,若
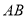 不平行
不平行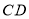 ,
,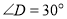 ,
,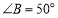 ,则
,则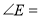 _______.
_______.(3)在总结前两问的基础上,借助图3,探究
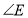 与
与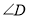 、
、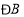 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸上的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形.在建立平面直角坐标系后,点B的坐标为(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,画出△A1B 1C1并写出点A1的坐标;
(2)把△ABC绕点C按顺时针旋转90°后得到△A2B2C,画出△A2B2C的图形并写出点A2的坐标.

相关试题

