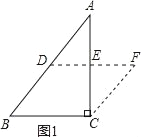
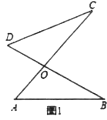
【题目】在△ABC中,沿图示的中位线DE剪一刀,拼成如图1所示的平行四边形BCFD.请仿上述方法,按要求完成下列操作设计,并在规定位置画出图示:
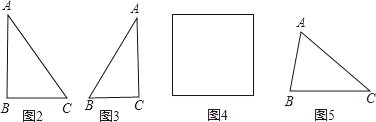
(1)在△ABC中,若∠C=90°,沿着中位线剪一刀,可拼成矩形或等腰梯形,请将拼成的图形画在图2位置(只需画一个);
(2)在△ABC中,若AB=2BC,沿着中位线剪一刀,可拼成菱形,并将拼成的图形画在图3位置;
(3)在△ABC中,需增加什么条件,沿着中位线剪一刀,拼成正方形,并将拼成的图形和符合条件的三角形一同画在图4位置;
(4)在△ABC中,若沿着某条线剪一刀,能拼成等腰梯形,请将拼成的图形画在图5位置(保留寻求剪裁线的痕迹).
参考答案:
【答案】(1)如图所示见解析;(2)如图所示见解析;(3)需增加条件:∠C=90°,AC=2BC,如图所示见解析;(4)如图所示见解析.
【解析】
(1)根据三角形的中位线定理可得△CDF≌△AEF,由∠C=90°,则四边形BCDE为矩形;(2)根据三角形的中位线定理可得△CEF≌△ADF,由AB=2BC,则,BC=BD,则四边形BCDE为菱形;(3)根据三角形的中位线定理可得△BEF≌△ADF,由∠C=90°,AB=2BC,则四边形BCDE为正方形;(4)沿GH剪一刀,使HB=HG,再过点A作AD∥BC,找出AC中点E,过E作DF平行HG,得到DF=AB,四边形ABFD为等腰梯形.
(1)如图;
(2)如图;
(3)需增加条件:∠C=90°,AC=2BC,如图;
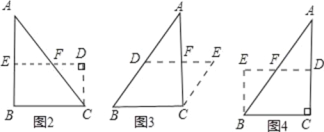
(4)如图,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
分组/元
频数
频率
1000<x<1200
3
0.060
1200<x<1400
12
0.240
1400<x<1600
18
0.360
1600<x<1800
a
0.200
1800<x<2000
5
b
2000<x<2200
2
0.040
合计
50
1.000

请你根据以上提供的信息,解答下列问题:
(1)补全频数分布表a= , b= , 和频数分布直方图;
(2)这50个家庭电费支出的中位数落在哪个组内?
(3)若该地区有3万个家庭,请你估计该地区有多少个一年电费支出低于1400元的家庭? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
-
科目: 来源: 题型:
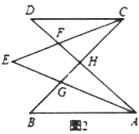
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,连接对角线BD,作AE⊥BD于E,CF⊥BD于F,
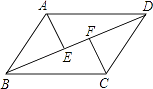
(1)求证:△AED≌△CFB;
(2)若∠ABC=75°,∠ADB=30°,AE=3,求平行四边形ABCD的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】小学我们已经知道三角形三个内角和是180°,对于如图1中,
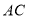 ,
,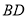 交于
交于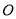 点,形成的两个三角形中的角存在以下关系:①
点,形成的两个三角形中的角存在以下关系:①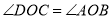 ;②
;②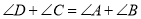 .试探究下面问题:
.试探究下面问题:已知
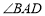 的平分线
的平分线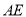 与
与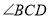 的平分线
的平分线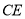 交于点
交于点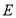 ,
,
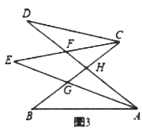
(1)如图2,若
 ,
,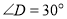 ,
,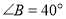 ,则
,则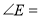 _________;
_________;(2)如图3,若
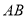 不平行
不平行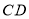 ,
,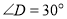 ,
,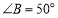 ,则
,则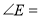 _______.
_______.(3)在总结前两问的基础上,借助图3,探究
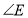 与
与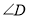 、
、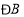 之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
之间是否存在某种等量关系?若存在,请说明理由;若不存在,请举例说明.
相关试题

