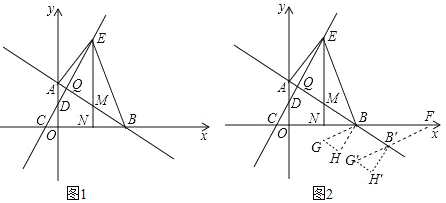
【题目】如图1,在平面直角坐标系中,直线AB与y轴交于点![]() ,与x轴交于点B,
,与x轴交于点B,![]() ,直线CD与y轴交于点D,与x轴交于点
,直线CD与y轴交于点D,与x轴交于点![]() ,
,![]() ,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
,直线AB与直线CD交于点Q,E为直线CD上一动点,过点E作x轴的垂线,交直线AB于点M,交x轴于点N,连接AE、BE.
![]() 求直线AB、CD的解析式及点Q的坐标;
求直线AB、CD的解析式及点Q的坐标;
![]() 当E点运动到Q点的右侧,且
当E点运动到Q点的右侧,且![]() 的面积为
的面积为![]() 时,在y轴上有一动点P,直线AB上有一动点R,当
时,在y轴上有一动点P,直线AB上有一动点R,当![]() 的周长最小时,求点P的坐标及
的周长最小时,求点P的坐标及![]() 周长的最小值.
周长的最小值.
![]() 在
在![]() 问的条件下,如图2将
问的条件下,如图2将![]() 绕着点B逆时针旋转
绕着点B逆时针旋转![]() 得到
得到![]() ,使点M与点G重合,点N与点H重合,再将
,使点M与点G重合,点N与点H重合,再将![]() 沿着直线AB平移,记平移中的
沿着直线AB平移,记平移中的![]() 为
为![]() ,在平移过程中,设直线
,在平移过程中,设直线![]() 与x轴交于点F,是否存在这样的点F,使得
与x轴交于点F,是否存在这样的点F,使得![]() 为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
为等腰三角形?若存在,求出此时点F的坐标;若不存在,说明理由
参考答案:
【答案】(1)点Q坐标为![]() ;(2)
;(2)![]() 周长的最小值,最小值为
周长的最小值,最小值为![]() ;(3)点F的坐标为
;(3)点F的坐标为![]() .
.
【解析】
![]() ,直线CD表达式的k值为
,直线CD表达式的k值为![]() ,即可求解直线CD的表达式;同理可得直线AB的表达式,联立两个表达式,即可求解点Q的坐标;
,即可求解直线CD的表达式;同理可得直线AB的表达式,联立两个表达式,即可求解点Q的坐标;
![]() ,求出点N坐标;作N点的两个对称点
,求出点N坐标;作N点的两个对称点![]() 、
、![]() ,连接
,连接![]() 交AB于点R交y轴于点P,此时,
交AB于点R交y轴于点P,此时,![]() 周长的最小值,求解即可;
周长的最小值,求解即可;
![]() 是底角为
是底角为![]() 的当腰三角形,
的当腰三角形,![]() 为等腰三角形,即可求解.
为等腰三角形,即可求解.
![]() 点
点![]() ,
,![]() ,
,![]() ,直线CD表达式的k值为
,直线CD表达式的k值为![]() ,
,
则直线CD的表达式为:![]() ,将点C坐标代入上式并解得:
,将点C坐标代入上式并解得:![]() ,
,
故:直线CD的表达式为:![]() ,
,
同理可得直线AB的表达式为:![]() ,
,![]() ,
,
联立![]() 并解得:
并解得:![]() ,即点Q坐标为
,即点Q坐标为![]() ;
;
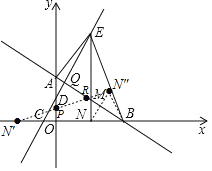
![]() 如图所示,设点E的坐标为
如图所示,设点E的坐标为![]() ,则点
,则点![]() ,
,
![]() ,
,
解得:![]() ,即点N坐标为
,即点N坐标为![]() ,点
,点![]() ,
,
作点N关于直线AB和y轴的对称点![]() 、
、![]() ,连接
,连接![]() 交AB于点R交y轴于点P,
交AB于点R交y轴于点P,
此时,![]() 周长的最小值,最小值为:
周长的最小值,最小值为:![]() 的长度,
的长度,
![]() ,
,![]() 关于直线AB对称,
关于直线AB对称,![]() ,
,
![]() 为边长为3的等边三角形,三角形高为:
为边长为3的等边三角形,三角形高为:![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,
则直线![]() 的表达式为:
的表达式为:![]() ,即点P坐标
,即点P坐标![]() ,
,
![]() 周长的最小值,最小值为
周长的最小值,最小值为![]() ;
;
![]() 如图2,将
如图2,将![]() 绕着点B逆时针旋转
绕着点B逆时针旋转![]() 得到
得到![]() ,
,
此时![]() ,即点GM关于x轴对称,则点
,即点GM关于x轴对称,则点![]() ,
,![]() ,
,
图形平移为![]() 时,
时,![]() ,
,
即![]() 是底角为
是底角为![]() 的等腰三角形,而
的等腰三角形,而![]() 为等腰三角形,只能
为等腰三角形,只能![]() ,
,
![]() ,
,![]() ,
,
故点F的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:ABC平移后得出△A1B1C1,点A(﹣1,3)平移后得A1(﹣4,2),又已知B1(﹣2,3),C1(1,﹣1),求B、C坐标,画图并说明经过了怎样的平移.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在梯形ABCD中,AB∥CD,∠B=90°,AB=2,CD=1,BC=m,P为线段BC上的一动点,且和B、C不重合,连接PA,过P作PE⊥PA交CD所在直线于E.设BP=x,CE=y.

(1)求y与x的函数关系式;
(2)若点P在线段BC上运动时,点E总在线段CD上,求m的取值范围;
(3)如图2,若m=4,将△PEC沿PE翻折至△PEG位置,∠BAG=90°,求BP长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
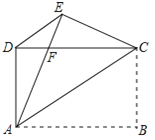
(1)求证:△DEC≌△EDA;
(2)求DF的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示:
(1)直接写出点A的坐标,点A关于x轴的对称点B的坐标,点B关于y轴的对称点C的坐标.
(2)画出将线段BC向右平移2个单位,再向上平移4个单位后的线段B′C′,并直接写出B′的坐标.
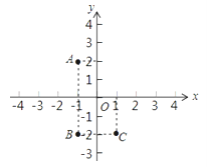
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2
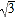 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.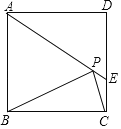
相关试题

