搜索
【题目】如图，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．
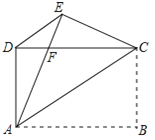
（1）求证：△DEC≌△EDA；
（2）求DF的值；
参考答案：
【答案】见解析
【解析】
试题（1）由矩形和翻折的性质可知AD=CE，DC=EA，根据“SSS”可求得△DEC≌△EDA；
（2）根据勾股定理即可求得
试题解析：（1）由矩形的性质可知△ADC≌△CEA，
∴AD=CE，DC=EA，∠ACD=∠CAE，
在△ADE与△CED中
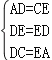
∴△DEC≌△EDA（SSS）；
（2）∵∠ACD=∠CAE，
∴AF=CF，
设DF=x，则AF=CF=4﹣x，
在RT△ADF中，AD2+DF2=AF2，
即32+x2=（4﹣x）2，
解得；x=
，
即DF=．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：ABC平移后得出△A1B1C1，点A（﹣1，3）平移后得A1（﹣4，2），又已知B1（﹣2，3），C1（1，﹣1），求B、C坐标，画图并说明经过了怎样的平移．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在梯形ABCD中，AB∥CD，∠B=90°，AB=2，CD=1，BC=m，P为线段BC上的一动点，且和B、C不重合，连接PA，过P作PE⊥PA交CD所在直线于E．设BP=x，CE=y．
（1）求y与x的函数关系式；
（2）若点P在线段BC上运动时，点E总在线段CD上，求m的取值范围；
（3）如图2，若m=4，将△PEC沿PE翻折至△PEG位置，∠BAG=90°，求BP长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线AB与y轴交于点
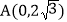，与x轴交于点B，
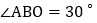，直线CD与y轴交于点D，与x轴交于点
，
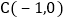，直线AB与直线CD交于点Q，E为直线CD上一动点，过点E作x轴的垂线，交直线AB于点M，交x轴于点N，连接AE、BE．
求直线AB、CD的解析式及点Q的坐标；
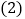当E点运动到Q点的右侧，且
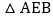的面积为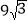
时，在y轴上有一动点P，直线AB上有一动点R，当
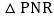的周长最小时，求点P的坐标及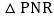周长的最小值．
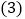在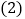问的条件下，如图2将
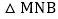绕着点B逆时针旋转
得到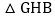
，使点M与点G重合，点N与点H重合，再将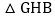沿着直线AB平移，记平移中的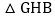为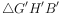
，在平移过程中，设直线
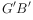与x轴交于点F，是否存在这样的点F，使得
为等腰三角形？若存在，求出此时点F的坐标；若不存在，说明理由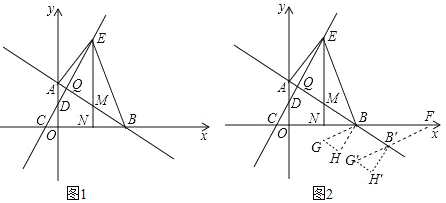
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示：
（1）直接写出点A的坐标，点A关于x轴的对称点B的坐标，点B关于y轴的对称点C的坐标.
（2）画出将线段BC向右平移2个单位，再向上平移4个单位后的线段B′C′，并直接写出B′的坐标．
-
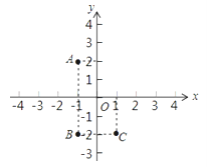
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AD=2
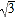，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为___．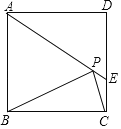
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，张三打算在院落种上蔬菜．已知院落为东西长为32米，南北宽为20米的长方形，为了行走方便，要修筑同样宽度的三条小路，东西两条，南北一条，余下的部分种上各类蔬菜．若每条小路的宽均为1米．
（1）求蔬菜的种植面积；
（2）若每平方米的每季蔬菜的值为3元，成本为1元，这个院落每季的产值是多少？
相关试题
