【题目】如图,长方形纸片![]() 中,
中,![]() ,将纸片折叠,使顶点
,将纸片折叠,使顶点![]() 落在边
落在边![]() 上的
上的![]() 点处,折痕的一端
点处,折痕的一端![]() 点在边
点在边![]() 上.
上.
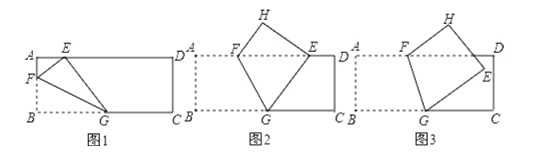
(1)如图1,当折痕的另一端![]() 在
在![]() 边上且
边上且![]() 时,求
时,求![]() 的长
的长
(2)如图2,当折痕的另一端![]() 在
在![]() 边上且
边上且![]() 时,
时,
①求证:![]() .②求
.②求![]() 的长.
的长.
(3)如图3,当折痕的另一端![]() 在
在![]() 边上,
边上,![]() 点的对应点
点的对应点![]() 在长方形内部,
在长方形内部,![]() 到
到![]() 的距离为2
的距离为2![]() ,且
,且![]() 时,求
时,求![]() 的长.
的长.
参考答案:
【答案】(1)3;(2)①证明见解析;②6;(3)![]() .
.
【解析】
(1)根据翻折的性质可得BF=EF,然后用AF表示出EF,在Rt△AEF中,利用勾股定理列出方程求解即可;
(2)①根据翻折的性质可得∠BGF=∠EGF,再根据两直线平行,内错角相等可得∠BGF=∠EFG,从而得到∠EGF=∠EFG,再根据等角对等边证明即可;
②根据翻折的性质可得EG=BG,HE=AB,FH=AF,然后在Rt△EFH中,利用勾股定理列式计算即可得解;
(3)设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
(1)纸片折叠后顶点![]() 落在边
落在边![]() 上的
上的![]() 点处,
点处,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ;
;
(2)①∵纸片折叠后顶点![]() 落在边
落在边![]() 上的
上的![]() 点处,
点处,
∴![]() ,
,
∵长方形纸片![]() 的边
的边![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵纸片折叠后顶点![]() 落在边
落在边![]() 上的
上的![]() 点处,
点处,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ;
;
(3)法一:如图3,设![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
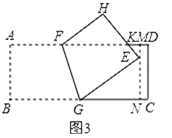
∵![]() 到
到![]() 的距离为2cm,
的距离为2cm,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
即![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
即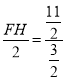 ,
,
解得![]() ,
,
∴![]() .
.
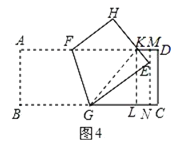
法二:如图4,设![]() 与
与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵![]() 到
到![]() 的距离为2
的距离为2![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
设![]() ,
,
在![]() 中,根据勾股定理可得:
中,根据勾股定理可得:![]() ,
,
在![]() 中,根据勾股定理可得:
中,根据勾股定理可得:![]() ,
,
在![]() 中,根据勾股定理可得:
中,根据勾股定理可得:![]() ,
,
即![]() ,解得:
,解得:![]() ,故
,故![]() ,
,
∴![]() ,
,
设![]() ,
,
在![]() 中,根据勾股定理可得:
中,根据勾股定理可得:![]() ,
,
∵![]()
即:![]() ,
,
解得:![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在
 和
和 中,
中, 为
为 边
边 上一点,
上一点, 平分
平分 ,
,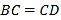 ,
, .
. 
(1)求证:

(2)如图(2),若
 ,连接
,连接 交
交 于
于 ,
, 为边
为边 上一点,满足
上一点,满足 ,连接
,连接 交
交 于
于 . ①求
. ①求 的度数;
的度数; ②若
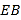 平分
平分 ,试说明:
,试说明: 平分
平分 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
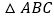 的边
的边 为直径画圆,与边
为直径画圆,与边 交于
交于 ,与边
,与边 交于
交于 ,已知
,已知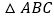 的面积是
的面积是 面积的
面积的 倍,
倍,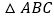 中有一个内角度数是另一内角度数的
中有一个内角度数是另一内角度数的 倍,试计算
倍,试计算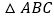 三个内角的度数:________.
三个内角的度数:________.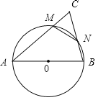
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知扇形
 中,
中, ,弦
,弦 ,点
,点 是弧
是弧 上任意一点(与端点
上任意一点(与端点 、
、 不重合),
不重合), 于点
于点 ,以点
,以点 为圆心、
为圆心、 长为半径作
长为半径作 ,分别过点
,分别过点 、
、 作
作 的切线,两切线相交于点
的切线,两切线相交于点 .
. 求弧
求弧 的长;
的长; 试判断
试判断 的大小是否随点
的大小是否随点 的运动而改变?若不变,请求出
的运动而改变?若不变,请求出 的大小;若改变,请说明理由.
的大小;若改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中,不能证明△ABC ≌ △DCB是( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】北京时间2015年7月31日,国际奥委会主席巴赫宣布:中国北京获得2022年第24届冬季奥林匹克运动会举办权.北京也创造历史,成为第一个既举办过夏奥会又举办冬奥会的城市,张家口也成为本届冬奥会的协办城市.近期,新建北京至张家口铁路可行性研究报告已经获得国家发改委批复,同意新建北京至张家口铁路,铁路全长约180千米.按照设计,京张高铁列车的平均行驶速度是普通快车的1.5倍,用时比普通快车用时少了20分钟,求高铁列车的平均行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 内接于
内接于 ,
,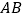 是直径,
是直径, 的切线
的切线 交
交 的延长线于点
的延长线于点 ,
, 交
交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .
.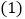 判断
判断 与
与 的位置关系并说明理由;
的位置关系并说明理由; 若
若 的半径为
的半径为 ,
,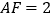 ,求
,求 的长.
的长.
相关试题

