【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(Ⅲ) 无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() .
.
【解析】(Ⅰ)把点A(1,0)代入![]() 求出m的值,从而确定二次函数解析式,进而求出顶点P的坐标;
求出m的值,从而确定二次函数解析式,进而求出顶点P的坐标;
(Ⅱ)先由函数解析式得出顶点坐标为![]() .再结合已知条件可知
.再结合已知条件可知![]() ,从而求出
,从而求出![]() ,
,![]() .再进行分类讨论得到抛物线解析式为
.再进行分类讨论得到抛物线解析式为![]() ;
;
(Ⅲ)由![]()
![]() 可知,定点H的坐标为
可知,定点H的坐标为![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,则可证
,则可证![]() .得点
.得点![]() 的坐标为
的坐标为![]() 或
或![]() .然后进行分类讨论即可求解.
.然后进行分类讨论即可求解.
(Ⅰ)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为![]() .
.
∵![]()
![]() ,
,
∴顶点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)抛物线![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
由点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴下方,
轴下方,![]() ,知点
,知点![]() 在第四象限.
在第四象限.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
可知![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 不在第四象限,舍去.
不在第四象限,舍去.
∴![]() .
.
∴抛物线解析式为![]() .
.
(Ⅲ)由![]()
![]() 可知,
可知,
当![]() 时,无论
时,无论![]() 取何值,
取何值,![]() 都等于4.
都等于4.
得点![]() 的坐标为
的坐标为![]() .
.
过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() .
.
∵![]()
![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
可得点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,可得直线
时,可得直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在直线
在直线![]() 上,
上,
∴![]() .解得
.解得![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 与点
与点![]() 重合,不符合题意,∴
重合,不符合题意,∴![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,
时,
可得直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在直线
在直线![]() 上,
上,
∴![]()
![]() .解得
.解得![]() (舍),
(舍),![]() .
.
∴![]() .
.
综上,![]() 或
或![]() .
.
故抛物线解析式为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:

(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
-
科目: 来源: 题型:
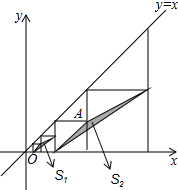
查看答案和解析>>【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数
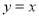 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为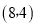 ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为 、
、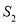 、
、 、
、 、
、 ,则
,则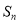 的值为______
的值为______ 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知A.B是直线上的两点,且AB=6,若P在这条直线上,且PA=5.
①画出P点在直线AB上的大致位置图;
②求PB长.
(2)尺规作图(不写作法.保留作图痕迹)
已知线段
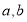 ,求作:线段MN,使MN=
,求作:线段MN,使MN=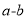 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
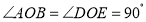 ,OC是BO的延长线,OF平分∠AOD,∠AOE=35.
,OC是BO的延长线,OF平分∠AOD,∠AOE=35.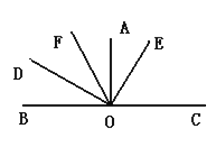
(1)求∠EOC的度数;
(2)求∠BOF的度数;
(3)请你写出图中三对相等的角.
相关试题

