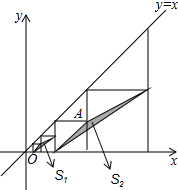
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()
参考答案:
【答案】![]()
【解析】分析:
由题意可知Sn是第2n个正方形和第(2n-1)个正方形之间的阴影部分,先由已知条件分别求出图中第1个、第2个、第3个和第4个正方形的边长,并由此计算出S1、S2,并分析得到Sn与n间的关系,这样即可把Sn给表达出来了.
详解:
∵函数y=x与x轴的夹角为45°,
∴直线y=x与正方形的边围成的三角形是等腰直角三角形,
∵A(8,4),
∴第四个正方形的边长为8,
第三个正方形的边长为4,
第二个正方形的边长为2,
第一个正方形的边长为1,
…,
第n个正方形的边长为![]() ,第(n-1)个正方形的边长为
,第(n-1)个正方形的边长为![]() ,
,
由图可知,S1=![]() ,
,
S2=![]() ,
,
…,
由此可知Sn=第(2n-1)个正方形面积的一半,
∵第(2n-1)个正方形的边长为![]() ,
,
∴Sn=![]() .
.
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数
10
15
20
…
x
方式一的总费用(元)
150
175
______
…
______
方式二的总费用(元)
90
135
______
…
______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,四边形
 是矩形,点
是矩形,点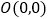 ,点
,点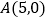 ,点
,点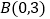 .以点
.以点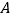 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形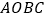 ,得到矩形
,得到矩形 ,点
,点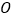 ,
,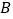 ,
,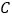 的对应点分别为
的对应点分别为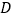 ,
,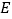 ,
,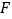 .
.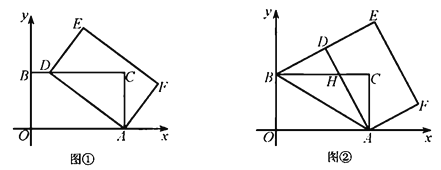
(Ⅰ)如图①,当点
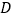 落在
落在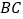 边上时,求点
边上时,求点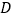 的坐标;
的坐标;(Ⅱ)如图②,当点
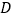 落在线段
落在线段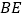 上时,
上时,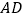 与
与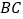 交于点
交于点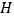 .
.①求证
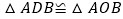 ;
;②求点
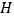 的坐标.
的坐标.(Ⅲ)记
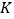 为矩形
为矩形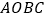 对角线的交点,
对角线的交点,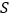 为
为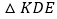 的面积,求
的面积,求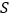 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:

(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
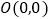 ,点
,点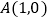 .已知抛物线
.已知抛物线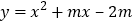 (
(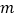 是常数),顶点为
是常数),顶点为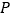 .
.(Ⅰ)当抛物线经过点
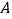 时,求顶点
时,求顶点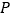 的坐标;
的坐标;(Ⅱ)若点
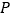 在
在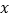 轴下方,当
轴下方,当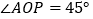 时,求抛物线的解析式;
时,求抛物线的解析式;(Ⅲ) 无论
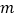 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点 .当
.当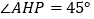 时,求抛物线的解析式.
时,求抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知A.B是直线上的两点,且AB=6,若P在这条直线上,且PA=5.
①画出P点在直线AB上的大致位置图;
②求PB长.
(2)尺规作图(不写作法.保留作图痕迹)
已知线段
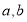 ,求作:线段MN,使MN=
,求作:线段MN,使MN=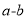 .
.
相关试题

