【题目】某文具店今年1月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.
(1)若该种笔记本在2月份的销售量不低于2200本,则2月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比中2月份在(1)的条件下的最高售价减少了 ![]() m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
m%,结果3月份的销量比2月份在(1)的条件下的最低销量增加了m%,3月份的销售利润达到6600元,求m的值.
参考答案:
【答案】
(1)解:设售价应为x元,依题意得:
2290﹣15(x﹣11)÷0.5≥2200,
解得x≤14.
答:2月份售价应不高于14元
(2)解:[14(1﹣ ![]() m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,
m%)﹣10(1+10%)]×2200(1+m%)=6600,令m%=t,
原式为(3﹣2t)(1+t)=3.
t1=0(不合题意,舍去),t2=0.5,
∴m=50.
答:m的值是50.
【解析】(1)由“销售量不低于2200”可列出不等式2290﹣15(x﹣11)÷0.5≥2200,求出售价的最高值;(2)根据销售利润=单件利润![]() 销售量,用m的代数式分别表示售价,进价,销售利润,列出方程即可.
销售量,用m的代数式分别表示售价,进价,销售利润,列出方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图).
(1)CE∥BF这一结论对吗?为什么?
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)的图象与反比例函数y=
 (k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(k≠0)的图象相交于A,B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(﹣1,0),点A的横坐标是1,tan∠CDO=2.过点B作BH⊥y轴交y轴于H,连接AH.
(1)求一次函数和反比例函数的解析式;
(2)求△ABH面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x﹣3)2+
 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
A.①③
B.①④
C.①③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
-
科目: 来源: 题型:
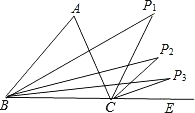
查看答案和解析>>【题目】如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的交点…依此类推,则∠Pn=( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.
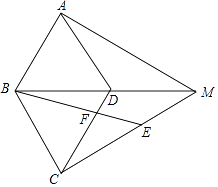
(1)若∠AMB=30°,且DM=3,求BE的长;
(2)证明:AM=CF+DM.
相关试题

