【题目】探究与发现:如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.

(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系.
参考答案:
【答案】(1)∠EDC=30°.(2)∠CDE =![]() ∠BAD.理由见解析.
∠BAD.理由见解析.
【解析】
(1)先根据等腰直角三角形的性质得到∠B=∠C=45°,根据三角形外角的性质和已知各角的度数得出∠ADC=∠B+∠BAD=105°,再根据三角形外角的性质得到∠AED=∠C+∠EDC,则结合题意可得∠ADC-∠EDC=105°-∠EDC=45°+∠EDC,解得∠EDC=30°.
(2)由AE=AD,得到∠ADE=∠AED,设∠BAD=x.根据三角形外角的性质得到∠ADC=∠B+∠BAD=45°+x和∠AED=∠C+∠EDC,结合题意得到∠EDC=![]() ∠BAD.
∠BAD.
(1)∵在Rt△ABC中,∠BAC=90°,AB=AC,
则∠B=∠C=45°,
又∵∠ADC是△ABD的外角,∠BAD=60°,
∴∠ADC=∠B+∠BAD=105°.
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=105°-∠EDC=45°+∠EDC,
解得:∠EDC=30°.
(2)∠CDE=![]() ∠BAD.
∠BAD.
理由如下:
∵AE=AD,
则∠ADE=∠AED,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=45°+∠BAD
∵∠AED是△CDE的外角,
∴∠AED=∠EDC +∠C=∠EDC+45°,
∵∠B=∠C=45°,∠ADE=∠AED,
∴∠ADE=∠ADC-∠EDC=45°+∠BAD-∠EDC=45°+∠EDC,
解得:∠EDC =![]() ∠BAD,.故∠CDE=
∠BAD,.故∠CDE=![]() ∠BAD.
∠BAD.
-
科目: 来源: 题型:
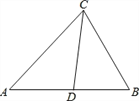
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.
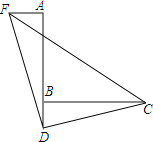
(1)求证:△FAD≌△DBC;
(2)判断△CDF的形状并证明.
-
科目: 来源: 题型:
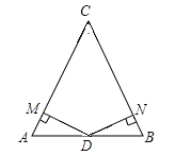
查看答案和解析>>【题目】如图,在△ABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)AC=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=
 S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:
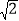 ≈1.414,
≈1.414, ≈1.732)
≈1.732)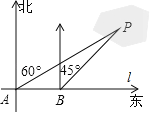
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式:
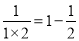 ,
,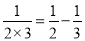 ,
,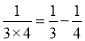 ,将以上三个等式两边分别相加得:
,将以上三个等式两边分别相加得: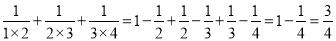 .
.(1)观察发现:
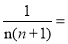 __________
__________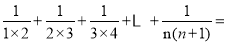 .
.(2)初步应用:利用(1)的结论,解决以下问题“①把
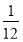 拆成两个分子为1的正的真分数之差,即
拆成两个分子为1的正的真分数之差,即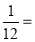 ;②把
;②把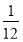 拆成两个分子为1的正的真分数之和,即
拆成两个分子为1的正的真分数之和,即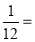 ;
;( 3 )定义“
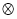 ”是一种新的运算,若
”是一种新的运算,若 ,
,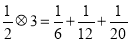 ,
,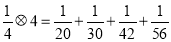 ,求
,求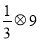 的值.
的值.
相关试题

