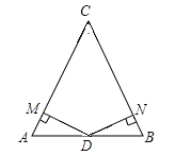
【题目】如图,在△ABC中,D是AB的中点,DM⊥AC于点M,DN⊥BC于点N,且DM=DN.
(1)求证:AM=BN;
(2)AC=BC.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
对于(1),连接CD,利用HL定理,先证明△DAM≌△DBN,再由全等三角形对应边相等求得结论;
对于(2),由DM=DN且DM⊥AC于M,DN⊥BC于N,可证得Rt△CDM≌Rt△CDN,则CM=CN,再由(1)的结论即可得证.
证明:(1)连接CD,如图所示,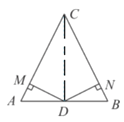
∵D是AB的中点,
∴AD=BD.
又∵DM=DN且DM⊥AC于M,DN⊥BC于N,
∴△DAM≌△DBN(HL),
∴AM=BN.
(2)∵DM=DN且DM⊥AC于M,DN⊥BC于N,
∴Rt△CDM≌Rt△CDN(HL),
∴CM=CN,
∴AC=AM+CM,BC=BN+CN,
∴AC=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形
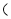 小长方形纸片长为a,宽为
小长方形纸片长为a,宽为 ,请你仔细观察图形,解答下列问题:
,请你仔细观察图形,解答下列问题:
(1)a和b之间的关系满足_____________________.
(2)图中阴影部分的面积与大长方形面积的比值是___________.
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法,请你写出
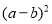 ,
,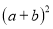 与
与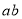 三个代数式之间的等量关系_________________________
三个代数式之间的等量关系_________________________应用:根据探索中的等量关系,解决如下问题:
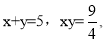 求
求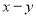 的值
的值 -
科目: 来源: 题型:
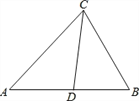
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.
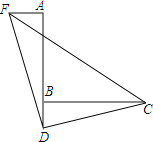
(1)求证:△FAD≌△DBC;
(2)判断△CDF的形状并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.

(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=
 S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:
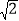 ≈1.414,
≈1.414,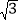 ≈1.732)
≈1.732)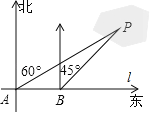
相关试题

