搜索
【题目】下列等式：
，
，
，将以上三个等式两边分别相加得：
．
（1）观察发现：
__________
．
（2）初步应用：利用（1）的结论，解决以下问题“①把
拆成两个分子为1的正的真分数之差，即
；②把拆成两个分子为1的正的真分数之和，即 ；
（ 3 ）定义“
”是一种新的运算，若
，
，
，求
的值．
参考答案：
【答案】（1）
；
；（2）①
；②
；（ 3 ）
．
【解析】
（1）利用材料中的“拆项法”解答即可；
（2）①先变形为
，再利用（1）中的规律解题；②先变形为
，再逆用分数的加法法则即可分解；
（3）按照定义“
”法则表示出
，再利用（1）中的规律解题即可．
解：（1）观察发现：
，
＝
＝
＝；
故答案是：；.
（2）初步应用：
①=
；
②
；
故答案是：；
.
（ 3 ）由定义可知：
＝
=
=
=.
故的值为．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究与发现：如图，在Rt△ABC中，∠BAC=90°，AB=AC，点D在底边BC上，AE=AD，连结DE.
（1）当∠BAD=60°时，求∠CDE的度数；
（2）当点D在BC （点B、C除外） 上运动时，试猜想并探究∠BAD与∠CDE的数量关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象经过点A（﹣2，6），且与x轴相交于点B，与正比例函数y=3x的图象相交于点C，点C的横坐标为1．
（1）求k、b的值；
（2）若点D在y轴负半轴上，且满足S△COD=
S△BOC，求点D的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离，某数学兴趣小组在公路l上的点A处，测得凉亭P在北偏东60°的方向上；从A处向正东方向行走200米，到达公路l上的点B处，再次测得凉亭P在北偏东45°的方向上，如图所示．求凉亭P到公路l的距离．（结果保留整数，参考数据：
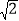≈1.414，
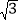≈1.732）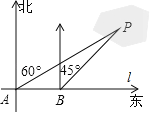
-
科目： 来源： 题型：
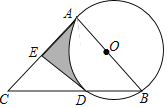
查看答案和解析>>【题目】如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．
（1）试判断直线DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为2，∠B=50°，AC=4.8，求图中阴影部分的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知多项式4x6y2- 3x2y- x- 7，次数是b，4a与b互为相反数，在数轴上，点A表示数a，点B表示数b．
（1）a=____________，b=____________
（2）若小蚂蚁甲从点A处以3个单位长度/秒的速度向左运动，同时小蚂蚁乙从点B处以4单位长度/秒的速度也向左运动，丙同学观察两只小蚂蚁运动，在它们刚开始运动时，在原点0处放置一颗饭粒，乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动，设运动的时间为t秒，求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t．（写出解答过程）
（3）若小蚂蚁甲和乙约好分别从A，B两点，分别沿数轴甲向左，乙向右以相同的速度爬行，经过一段时间原路返回，刚好在16s时一起重新回到原出发点A和B，设小蚂蚁们出发t（s）时的速度为v（mm/s），v与t之间的关系如下图．（其中s表示时间单位秒，mm表示路程单位毫米）
t （s）
0<t≤2
2<t≤5
5<t≤16
v（mm/s）
10
16
8
①当2<t≤5时，你知道小蚂蚁甲与乙之间的距离吗？（用含有t的代数式表示）；
②当t为__________________时，小蚂蚁甲乙之间的距离是42mm．（请直接写出答案）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在解决线段数量关系问题中，如果条件中有角平分线，经常采用下面构造全等三角形的解决思路.如：在图1中，若
是
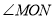的平分线
上一点，点
在
上，此时，在
截取
,连接
，根据三角形全等的判定
，容易构造出全等三角形⊿
和⊿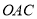
,参考上面的方法，解答下列问题：
如图2，在非等边⊿
中， 
, 
分别是
的平分线，且
交于点
.求证： 
.
相关试题
