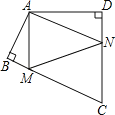
【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
参考答案:
【答案】70°
【解析】
延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD分别交于点M、N,此时△AMN周长最小,推出∠AMN+∠ANM=2(∠A′+∠A″),进而得出∠MAN的度数.
解:延长AB到A′使得BA′=AB,延长AD到A″使得DA″=AD,连接A′A″与BC、CD分别交于点M、N.
∵∠ABC=∠ADC=90°,
∴A、A′关于BC对称,A、A″关于CD对称,
此时△AMN的周长最小,
∵BA=BA′,MB⊥AB,
∴MA=MA′,同理:NA=NA″,
∴∠A′=∠MAB,∠A″=∠NAD,
∵∠AMN=∠A′+∠MAB=2∠A′,∠ANM=∠A″+∠NAD=2∠A″,
∴∠AMN+∠ANM=2(∠A′+∠A″),
∵∠BAD=125°,
∴∠A′+∠A″=180°﹣∠BAD=55°,
∴∠AMN+∠ANM=2×55°=110°.
∴∠MAN=180°﹣110°=70°,
故答案为:70°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2 cm时,这个六边形的周长为
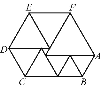
A. 30cm B. 40cm C. 50cm D. 60cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
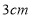 B.
B. 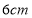 C.
C.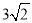
 D.
D. 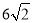
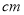

-
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
相关试题

