【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

参考答案:
【答案】(1)高铁的平均速度是每小时240千米;(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有56千米
【解析】
(1)利用图象给出的数量关系及关键的数值,从图象中可以得高铁运行的时间和行驶的路程,可得高铁的行驶速度;
(2)设私家车的速度为x千米/时,根据题意列方程解答即可.
解:(1)观察图象可得,高铁行驶的时间是1小时,行驶的路程是240千米.
所以240÷1=240(km/h),
故高铁的平均速度是每小时240千米.
(2)设私家车的速度为x千米/时,根据题意得:
1.5x=240×(1.5﹣1)
解得x=80.
∴当小颖到达乐山高铁站时,小明距乐山大佛景区距离为:216﹣80×2=56(km).
答:当小颖到达乐山高铁站时,小明距离乐山大佛景区还有56千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
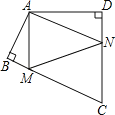
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
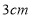 B.
B. 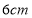 C.
C.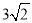
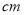 D.
D. 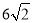
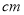

-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两点分别表示两幢大楼所在的位置,直线a表示输水总管道,直线b表示输煤气总管道.现要在这两根总管道上分别设一个连接点,安装分管道将水和煤气输送到A,B两幢大楼,要求使铺设至两幢大楼的输水分管道和输煤气分管道的用料最短.图中,点A'是点A关于直线b的对称点,A'B分别交直线b,a于点C,D;点B'是点B关于直线a的对称点,B'A分别交直线b,a于点E,F.则符合要求的输水和输煤气分管道的连接点依次是
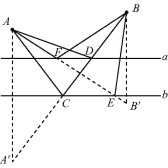
A. F和C B. F和E C. D和C D. D和E
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
相关试题

