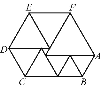
【题目】如图是由九个等边三角形组成的一个六边形,当最小的等边三角形边长为2 cm时,这个六边形的周长为
A. 30cm B. 40cm C. 50cm D. 60cm
参考答案:
【答案】D
【解析】
因为每个三角形都是等边的,从其中一个三角形入手,比右下角的以AB为边的三角形,设它的边长为x,则等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2.所以六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)="7" x+18,而最大的三角形的边长AF等于AB的2倍,所以可以求出x,则可求得周长.
设AB=x,
∴等边三角形的边长依次为x,x+x+2,x+2,x+2×2,x+2×2,x+3×2,
∴六边形周长是2x+2(x+2)+2(x+2×2)+(x+3×2)="7" x+18,
∵AF=2AB,即x+6=2x,
∴x=6cm,
∴周长为7 x+18=60cm.
故选D
-
科目: 来源: 题型:
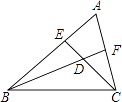
查看答案和解析>>【题目】如图,锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D.请写出图中的一对相似三角形,如 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为零.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
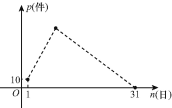
(1)写出p关于n的函数关系式 .(注明n的取值范围)
(2)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蓝莓种植生产基地产销两旺,采摘的蓝莓部分加工销售,部分直接销售,且当天都能销售完,直接销售是40元/斤,加工销售是130元/斤(不计损耗).已知基地雇佣20名工人,每名工人只能参与采摘和加工中的一项工作,每人每天可以采摘70斤或加工35斤.设安排x名工人采摘蓝莓,剩下的工人加工蓝莓.
(1)若基地一天的总销售收入为y元,求y与x的函数关系式;
(2)试求如何分配工人,才能使一天的销售收入最大?并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出该不等式组的整数解.
,并写出该不等式组的整数解. -
科目: 来源: 题型:
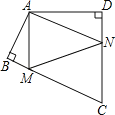
查看答案和解析>>【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )
A.
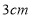 B.
B. 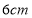 C.
C.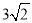
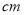 D.
D. 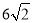

相关试题

