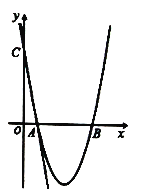
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 两点,与
两点,与![]() 轴交于另一点
轴交于另一点![]() .
.
(1)求抛物线解析式及![]() 点坐标;
点坐标;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上一动点,连接
为抛物线上一动点,连接![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求此时点
倍,求此时点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,
,![]()
![]() ,
,![]() ,见解析.
,见解析.
【解析】
(1)利用![]() 两点是一次函数上的点求出
两点是一次函数上的点求出![]() 两点,再代入二次函数求解即可.
两点,再代入二次函数求解即可.
(2)根据![]() ,
,![]() 求出
求出![]() ,求出△ABC.
,求出△ABC.
(3)根据![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,求出
倍,求出![]() ,得出
,得出![]() 求出此时M的坐标即可.
求出此时M的坐标即可.
(1)解:∵直线![]()
∴令![]() ,则
,则![]() ,解得
,解得![]()
∴![]()
令![]() ,则
,则![]() ,∴
,∴![]()
将点![]() ,
,![]() 代入
代入![]() 中得,
中得,
![]() ,解得
,解得![]()
∴抛物线的解析式为:![]() ;
;
令![]() ,则
,则![]() ,解得
,解得![]()
∴![]() .
.
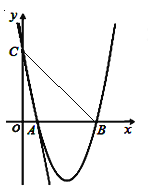
(2)解:∵![]() ,
,![]() ∴
∴![]()
∴![]()
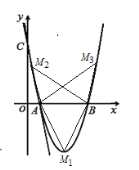
(3)∵![]() 面积为
面积为![]() 的面积的
的面积的![]() 倍,
倍,
∴![]()
∵AB=4 ,
∴![]() ,
,
∵![]()
∴抛物线的顶点坐标为![]() 符合条件,
符合条件,
当![]() 时,
时,![]() ,解的,x1=
,解的,x1=![]() ,x
,x![]() ,
,
∴![]() 点的坐标为
点的坐标为![]() (3,-4),
(3,-4),![]()
![]() ,
,![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1.
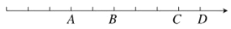
(1)如果点A、D表示的数互为相反数,那么点B表示的数是多少?
(2)当点B为原点时,若存在一点M到A点的距离是点M到D点的距离的2倍,则点M所表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知矩形
 中,点
中,点 是边
是边 上的一动点(不与点
上的一动点(不与点 、
、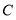 重合),过点
重合),过点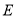 作
作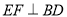 于点
于点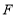 ,
,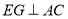 于点
于点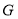 ,
,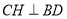 于点
于点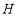 ,猜想线段
,猜想线段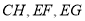 三者之间具有怎样的数量关系,并证明你的猜想;
三者之间具有怎样的数量关系,并证明你的猜想;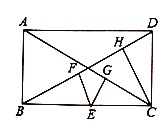
(2)如图,若点
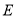 在矩形
在矩形 的边
的边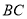 的延长线上,过点
的延长线上,过点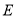 作
作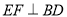 于点
于点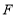 ,
,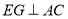 交
交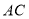 的延长线于点
的延长线于点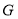 ,
,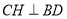 于点
于点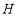 ,则线段
,则线段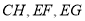 三者之间具有怎样的数量关系,直接写出你的结论;
三者之间具有怎样的数量关系,直接写出你的结论;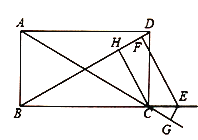
(3)如图,
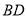 是正方形
是正方形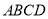 的对角线,
的对角线,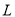 在
在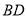 上,且
上,且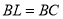 ,连接
,连接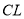 ,点
,点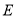 是
是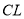 上任一点,
上任一点,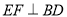 与点
与点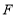 ,
,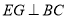 于点
于点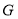 ,猜想线段
,猜想线段 之间具有怎样的数量关系,直接写出你的猜想.
之间具有怎样的数量关系,直接写出你的猜想.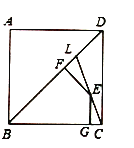
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
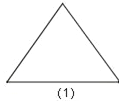
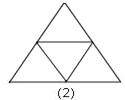
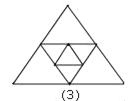
按上面方法继续下去,第20个图有_____个三角形;第n个图中有_____个三角形.(用n的代数式表示结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于O,
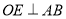 ,
,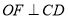 .
.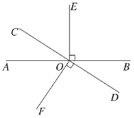
(1)①图中与
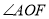 互余的角是______;
互余的角是______;②与
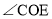 互补的角是______.(把符合条件的角都写出来)
互补的角是______.(把符合条件的角都写出来)(2)如果
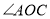 比
比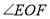 的
的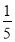 小
小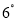 ,求
,求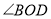 的度数.
的度数.
相关试题

