【题目】(1)如图,已知矩形![]() 中,点
中,点![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 三者之间具有怎样的数量关系,并证明你的猜想;
三者之间具有怎样的数量关系,并证明你的猜想;
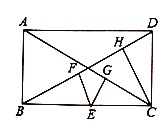
(2)如图,若点![]() 在矩形
在矩形![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 于点
于点![]() ,则线段
,则线段![]() 三者之间具有怎样的数量关系,直接写出你的结论;
三者之间具有怎样的数量关系,直接写出你的结论;
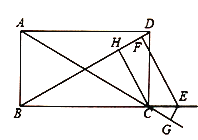
(3)如图,![]() 是正方形
是正方形![]() 的对角线,
的对角线,![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上任一点,
上任一点,![]() 与点
与点![]() ,
,![]() 于点
于点![]() ,猜想线段
,猜想线段![]() 之间具有怎样的数量关系,直接写出你的猜想.
之间具有怎样的数量关系,直接写出你的猜想.
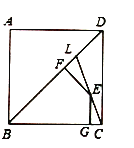
参考答案:
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() 或者
或者![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)过![]() 点作
点作![]() 于
于![]() ,先得出四边形
,先得出四边形![]() 是矩形,再证明四边形
是矩形,再证明四边形![]() 是矩形,证明
是矩形,证明![]() ,求出
,求出![]() 即可;
即可;
(2)过C点作CO垂直EF,可得矩形HCOF,因为HC=FO,只要证明EO=EG,最后根据AAS证明![]() .
.
(3)连接AC交BD于O,过点E作EH⊥AC,证明矩形FOHE,证明EG=CH,根据AAS证明![]() .
.
(1)答:![]()
证明:如图1,过![]() 点作
点作![]() 于
于![]() .
.
![]() ,
,

![]() 四边形
四边形![]() 是矩形.
是矩形.
![]() .
.
![]() .
.
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,且互相平分
,且互相平分
∴∠DBC=∠ACB
![]()
![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
∴EG=CN
![]() ;
;
即![]() ;
;
(2)![]() 或者
或者![]() ;
;
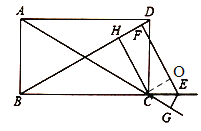
过C点作CO垂直EF,
∵![]() ,CO⊥EF,
,CO⊥EF,![]()
∴矩形COHF
∴CE∥BD,CH=DO
∴∠DBC=∠OCE
∵矩形ABCD
∴∠DBC=∠ACB
∵∠ECG=∠ACB
∴∠ECG=∠OCE
∵CO⊥EF,![]()
∴∠G=∠COE
∵CE=CE
∴![]()
∴EO=EG
∴![]() 或者
或者![]() ;
;
(3)![]() .
.

连接AC交BD于O,过点E作EH⊥AC,
∵正方形ABCD
∴FO⊥AC,![]()
∵EH⊥AC
∴矩形FEOH,∠EHC=90°
∵EG⊥BC,EF=OH
∴∠EGC=90°=∠EHC
∴EH∥BD
∴∠HEC=∠FLE
∵BL=BC
∴∠GCE=∠FLE
∴∠GCE=∠HEC
∵EC=EC
∴![]()
∴HC=GE
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于另一点Q,如果QP=QO,则∠OCP= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的单位长度为1.
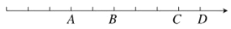
(1)如果点A、D表示的数互为相反数,那么点B表示的数是多少?
(2)当点B为原点时,若存在一点M到A点的距离是点M到D点的距离的2倍,则点M所表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
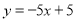 与
与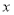 轴、
轴、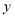 轴分别交于
轴分别交于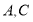 两点,抛物线
两点,抛物线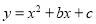 经过
经过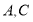 两点,与
两点,与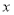 轴交于另一点
轴交于另一点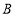 .
.(1)求抛物线解析式及
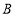 点坐标;
点坐标;(2)连接
 ,求
,求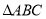 的面积;
的面积;(3)若点
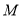 为抛物线上一动点,连接
为抛物线上一动点,连接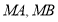 ,当点
,当点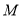 运动到某一位置时,
运动到某一位置时,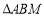 面积为
面积为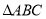 的面积的
的面积的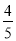 倍,求此时点
倍,求此时点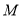 的坐标.
的坐标.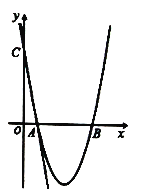
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
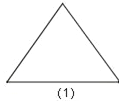
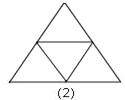
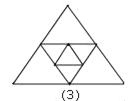
按上面方法继续下去,第20个图有_____个三角形;第n个图中有_____个三角形.(用n的代数式表示结论)
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

相关试题

