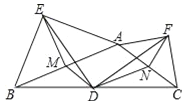
【题目】如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)首先根据D是BC中点,N是AC中点N,可得DN是△ABC的中位线,判断出DN=![]() AC;然后判断出EM=
AC;然后判断出EM=![]() AB,再通过证明四边形AMDN是平行四边形,可得∠AMD=∠AND,进而可证明∠EMD=∠DNF,由全等三角形的判定方法即可证明△EMD≌△DNF;
AB,再通过证明四边形AMDN是平行四边形,可得∠AMD=∠AND,进而可证明∠EMD=∠DNF,由全等三角形的判定方法即可证明△EMD≌△DNF;
(2)首先计算出EM:EA的值,DM和AF的数量关系以及证明∠EMD=∠EAF,再根据相似三角形判定的方法,判断出△EMD∽△∠EAF;
(3)由(2)可知△EMD∽△EAF,即可判断出∠MED=∠AEF,然后根据∠MED+∠AED=45°,判断出∠DEF=45°,再根据DE=DF,判断出∠DFE=45°,∠EDF=90°,即可判断出DE⊥DF.
试题解析:(1)∵D是BC中点,M是AB中点,N是AC中点,∴DM、DN都是△ABC的中位线,∴DM∥AC,且DM=![]() AC;DN∥AB,且DN=
AC;DN∥AB,且DN=![]() AB;
AB;
∵△ABE是等腰直角三角形,M是AB的中点,∴EM平分∠AEB,EM=![]() AB,∴EM=DN,同理:DM=FN,∵DM∥AC,DN∥AB,∴四边形AMDN是平行四边形,∴∠AMD=∠AND,又∵∠EMA=∠FNA=90°,∴∠EMD=∠DNF,在△EMD和△DNF中,∵EM=DN,∠EMD=∠DNF,MD=NF,∴△EMD≌△DNF;
AB,∴EM=DN,同理:DM=FN,∵DM∥AC,DN∥AB,∴四边形AMDN是平行四边形,∴∠AMD=∠AND,又∵∠EMA=∠FNA=90°,∴∠EMD=∠DNF,在△EMD和△DNF中,∵EM=DN,∠EMD=∠DNF,MD=NF,∴△EMD≌△DNF;
(2)∵三角形ABE是等腰直角三角形,M是AB的中点,∴EM平分∠AEB,EM⊥AB,∴EM=MA,∠EMA=90°,∠AEM=∠EAM=45°,∴![]() =sin45°=
=sin45°=![]() ,∵D是BC中点,M是AB中点,∴DM是△ABC的中位线,∴DM∥AC,且DM=
,∵D是BC中点,M是AB中点,∴DM是△ABC的中位线,∴DM∥AC,且DM=![]() AC;
AC;
∵△ACF是等腰直角三角形,N是AC的中点,∴FN=![]() AC,∠FNA=90°,∠FAN=∠AFN=45°,又∵DM=
AC,∠FNA=90°,∠FAN=∠AFN=45°,又∵DM=![]() AC,∴DM=FN=
AC,∴DM=FN=![]() FA,∵∠EMD=∠EMA+∠AMD=90°+∠AMD,∠EAF=360°﹣∠EAM﹣∠FAN﹣∠BAC=360°﹣45°﹣45°﹣(180°﹣∠AMD)=90°+∠AMD,∴∠EMD=∠EAF,在△EMD和△∠EAF中,∵
FA,∵∠EMD=∠EMA+∠AMD=90°+∠AMD,∠EAF=360°﹣∠EAM﹣∠FAN﹣∠BAC=360°﹣45°﹣45°﹣(180°﹣∠AMD)=90°+∠AMD,∴∠EMD=∠EAF,在△EMD和△∠EAF中,∵![]() ,∠EMD=∠EAF,∴△EMD∽△∠EAF;
,∠EMD=∠EAF,∴△EMD∽△∠EAF;
(3)∵△EMD∽△∠EAF,∴∠MED=∠AEF,∵∠MED+∠AED=45°,∴∠AED+∠AEF=45°,即∠DEF=45°,又∵△EMD≌△DNF,∴DE=DF,∴∠DFE=45°,∴∠EDF=180°﹣45°﹣45°=90°,∴DE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 面积相等的两个图形是全等图形 B. 全等三角形的周长相等
C. 所有正方形都是全等图形 D. 全等三角形的边相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读】
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,
其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
【运用】
利用“作差法”解决下列问题:
(1)小丽和小颖分别两次购买同一种商品,小丽两次都买了m千克商品,小颖两次购买商品均花费n元,已知第一次购买该商品的价格为a元/千克,第二次购买该商品的价格为b元/千克(a,b是整数,且a≠b),试比较小丽和小颖两次所购买商品的平均价格的高低.
(2)奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃了亏?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,D、E分别为等边三角形ABC边上的点,AD=CE,BD、AE交于N,BM⊥AE于M.
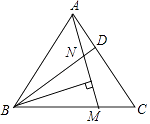
证明:
(1)∠CAE=∠ABD;
(2)MN= BN.
BN. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图坐标平面内,A(﹣2,0),B(0,﹣4),AB⊥AC,AB=AC,△ABC经过平移后,得△A′B′C′,B点的对应点B′(6,0),A,C对应点分别为A′,C′.
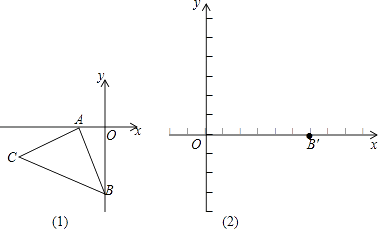
(1)求C点坐标;
(2)直接写出A′,C′坐标,并在图(2)中画出△A′B′C′;
(3)P为y轴负半轴一动点,以A′P为直角边以A’为直角顶点,在A′P右侧作等腰直角三角形A′PD.①试证明点D一定在x轴上;②若OP=3,求D点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边为4,另一边为9,则这个三角形的周长为( )
A. 17 B. 22 C. 13 D. 17或22
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2y+y-2值为3,则4y+2y+1的值为()
A.10B.3或11C.10或11D.11
相关试题

