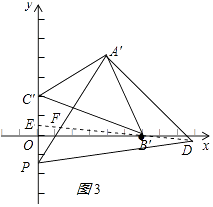
【题目】已知,如图坐标平面内,A(﹣2,0),B(0,﹣4),AB⊥AC,AB=AC,△ABC经过平移后,得△A′B′C′,B点的对应点B′(6,0),A,C对应点分别为A′,C′.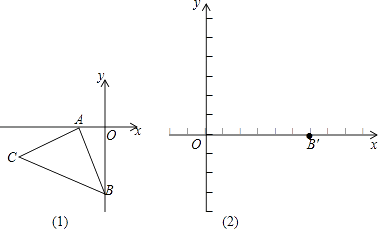
(1)求C点坐标;
(2)直接写出A′,C′坐标,并在图(2)中画出△A′B′C′;
(3)P为y轴负半轴一动点,以A′P为直角边以A’为直角顶点,在A′P右侧作等腰直角三角形A′PD.①试证明点D一定在x轴上;②若OP=3,求D点坐标.
参考答案:
【答案】
(1)
解:∵A(﹣2,0),B(0,﹣4),
∴AO=2,BO=4,
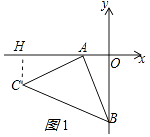
作CH⊥x轴于H,如图1所示:
则∠CHA=90°=∠AOB,
∴∠ACH+∠CAH=90°,
∵AB⊥AC,
∴∠BAO+∠CAH=90°,
∴∠ACH=∠BAO,
在△ACH和△BAO中, 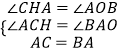 ,
,
∴△ACH≌△BAO(AAS),
∴AH=BO=4,CH=AO=2,
∴OH=AO+AH=6,
∴C(﹣6,﹣2)
(2)
解:∵B(0,﹣4),B′(6,0),
∴△ABC向上平移4个单位长度,再向右平移6个单位长度,
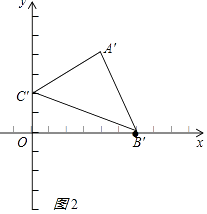
∴A′(4,4),C′(0,2)
(3)
解:①连B′D,延长DB′交PC′于E,交A′P于F,如图3所示:
∵△A′B′C′和△A′PD是等腰直角三角形,
∴A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,
∴∠PA′C′=∠DA′B′,
在:△A′DB′和△A′PC′中, 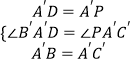 ,
,
∴△A′DB′≌△A′PC′(SAS),
∴∠A′DB′=∠A′PC′,
∵∠PFE=∠A′FD,
∴∠PEF=∠PA′D=90°,
∴DB′⊥y轴,
∴D点在x轴上;
②∵△A′DB′≌△A′PC′得,
∴B′D=C′P=5,
∴OD=11,
∴D(11,0).
【解析】(1)由点的坐标得出AO=2,BO=4,作CH⊥x轴于H,证出∠ACH=∠BAO,由AAS证明△ACH≌△BAO,得出AH=BO=4,CH=AO=2,求出OH=AO+AH=6,即可得出点C的坐标;C(﹣6,﹣2);(2)由B(0,﹣4)和B′(6,0),得出△ABC向上平移4个单位长度,再向右平移6个单位长度得△A′B′C′,即可得出A′,C′坐标,画出图形即可;(3)①连B′D,延长DB′交PC′于E,交A′P于F,由等腰直角三角形的性质得出A′B′=A′C′,A′P=A′D,∠B′A′C′=∠DA′P=90°,证出∠PA′C′=∠DA′B′,由SAS证明△A′DB′≌△A′PC′,得出∠A′DB′=∠A′PC′,由三角形内角和得出∠PEF=∠PA′D=90°,得出DB′⊥y轴,即可得出D点在x轴上;
②由全等三角形的性质得出B′D=C′P=5,得出OD=11,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【阅读】
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,
其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
【运用】
利用“作差法”解决下列问题:
(1)小丽和小颖分别两次购买同一种商品,小丽两次都买了m千克商品,小颖两次购买商品均花费n元,已知第一次购买该商品的价格为a元/千克,第二次购买该商品的价格为b元/千克(a,b是整数,且a≠b),试比较小丽和小颖两次所购买商品的平均价格的高低.
(2)奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃了亏?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,D、E分别为等边三角形ABC边上的点,AD=CE,BD、AE交于N,BM⊥AE于M.
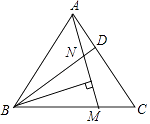
证明:
(1)∠CAE=∠ABD;
(2)MN= BN.
BN. -
科目: 来源: 题型:
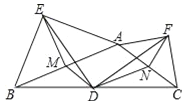
查看答案和解析>>【题目】如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边为4,另一边为9,则这个三角形的周长为( )
A. 17 B. 22 C. 13 D. 17或22
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知2y+y-2值为3,则4y+2y+1的值为()
A.10B.3或11C.10或11D.11
-
科目: 来源: 题型:
查看答案和解析>>【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=
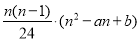 (其中a,b是常数,n≥4)
(其中a,b是常数,n≥4)(1)通过画图,可得:四边形时,P4= ;五边形时,P5= ;
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
相关试题

